Искусство орнамента содержит в неявном виде наиболее древнюю часть известной нам высшей математики. Герман Вейль – известный немецкий математик и физик-теоретик.
На прошлом занятии мы с вами говорили о линейных орнаментах – бордюрах.
Давайте возьмём бордюр из параллелограммов и применим к нему последовательно параллельный перенос так, чтобы образ этого бордюра с ним склеился. Если применить ещё и перенос в противоположном направлении, то копиями параллелограмма заполнится вся плоскость. Получилась конструкция, которая называется паркетом (или замощением).

Итак, плоский орнамент, заполняющий лист бумаги (плоскость) без промежутков и наложений частей, называется паркетом (или замощением).
Это такие же паркеты, как в наших квартирах, как орнаменты на линолеуме, как рисунки на обоях.
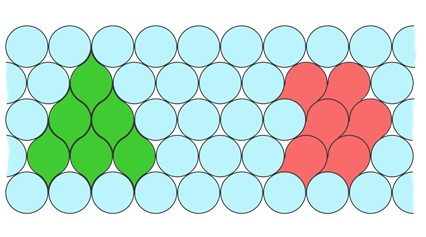
На следующем рисунке круги не образуют паркета, так как между ними есть промежутки, а вот зелёные и красные фигуры образуют.
Посмотрите на паркет, созданный голландским художником Маурицем Эшером.

Лебеди образуют, как говорят математики, «паркет». Кажется, что придумать такой затейливый орнамент невероятно сложно. И конечно же, без таланта здесь не обойтись. Но здесь нужны и некоторые геометрические знания и умения, овладев которыми, каждый сможет нарисовать свой неповторимый орнамент (паркет).
На паркете художника можно выделить элементарную ячейку (трафарет), параллельными переносами которой он получен.

Паркеты настолько часто встречаются в нашей жизни, что мы не замечаем их. Например, тетрадный лист в клеточку является примером паркета с квадратной ячейкой.

На этой решётке можно составить и другие паркеты. Например, за
элементарную ячейку можно взять и правильный треугольник. В этом случае
плоскость заполняется без промежутков путём поворота треугольников вокруг их
вершин на  .
.

Посмотрите на примеры ещё трёх паркетов.

Их можно назвать решётками.
В первом случае за элементарную ячейку взят прямоугольник размером 2 на 3 клетки. Во втором случае за элементарную ячейку взят параллелограмм, а в третьем – ромб.
А можно ли составить паркет из копий произвольного треугольник? Проверим. Изобразим произвольный треугольник. Положим с ним рядом такой же треугольник так, чтобы получился параллелограмм.

А параллелограммом можно замостить плоскость.
С помощью параллельных переносов можно получить паркет из параллелограммов одинаковым искривлением его сторон.

Из рассмотренных выше решёток можно сделать паркет с более замысловатыми ячейками.
Возьмём за основу квадратную решётку. Выделим ячейку размером 3 на 3 клетки. Проделаем с этой ячейкой-квадратом следующие операции.
Изменим верхнюю сторону квадрата. Тогда, чтобы ячейки «вдвинулись» одна в другую, так же надо изменить и противоположную сторону.
Затем к левой стороне квадрата пририсуем треугольник.
Такой же треугольник мы должны вырезать с противоположной стороны.

Получилась ячейка, которую теперь мы разрисуем.

Из получившейся фигурки сделаем вот такой паркет.

А сейчас давайте возьмём квадрат.

Вырежем из него два небольших кусочка и добавим их с противоположной стороны. Вырежем из него ещё два таких же кусочка и тоже добавим с противоположной стороны.

Раскрасив полученную фигуру в синий и красный цвета, сделаем вот такой паркет…

Теперь возьмём вот этот шестиугольник.

Выполним преобразования и получим…

Проявим немного воображения и раскрасим получившуюся фигуру двумя способами. Из получившихся фигурок сделаем вот такой паркет…

Используя тот же контур, но с другим рисунком, можно сделать ещё один паркет.

Если повернуть фигуру на  по часовой
стрелке и нарисовать мордочку собачки, то можно сделать вот такой паркет.
по часовой
стрелке и нарисовать мордочку собачки, то можно сделать вот такой паркет.

Очень интересные паркеты получаются, если на исходных фигурках имеется рисунок. Так, например, из треугольника получается неожиданный звёздный узор.

Все рассмотренные выше паркеты являются правильными.
Правильным называется такой паркет, который составлен повторением одной и той же фигуры. Иногда паркеты получаются и из фигур, которые не дают правильного паркета. Посмотрите на пятиугольник. Поворачивая и переворачивая его, можно построить разнообразные изображения.

Мы знаем, что параллелограммом можно замостить плоскость, используя две пары переносов в двух противоположных направлениях. Так же параллелепипедом можно замостить пространство. Только для этого придётся добавить ещё пару переносов в противоположных направлениях.

Замощение пространства (или его части) – это важная практическая задача. Например, при строительстве дома используют блоки или кирпичи. Понятно, что кирпич не может быть какой угодно формы. Его форма должна позволять соединять одинаковые кирпичи друг с другом так, чтобы не оставалось пустот. Самая простая и удобная для производства и строительства форма кирпича – форма прямоугольного параллелепипеда. Главное – это должны быть фигуры, которые могут без пустот заполнить пространство.
А сейчас посмотрим на следующие фигуры и выберем те, которые могут быть использованы для получения паркета.

Правильным шестиугольником можно замостить плоскость без промежутков и наложений.

А вот правильным пятиугольником не получится замостить плоскость без промежутков.
Следующая фигура напоминает параллелограмм с одинаковым искривлением двух его противоположных сторон. Ей мы сможем замостить плоскость без зазоров и наложений.


 Получите свидетельство
Получите свидетельство Вход
Вход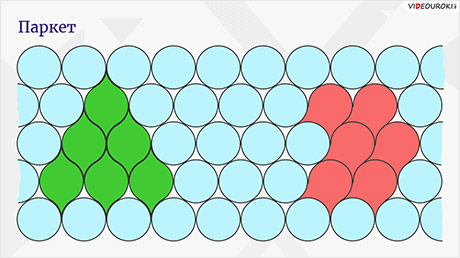




 3155
3155


