Здравствуйте, ребята!

Представляете, в школе юных математиков настоящий переполох – в третьем классе почти все ученики получили двойки за проверочную работу, в которой надо было решить особенные примеры.
А всё потому, что ребята не знали о том, как связаны между собой числа при делении. Я предложил им свою помощь и они, как и вы сейчас, смотрят на экран и готовы внимательно слушать. Так что, давайте скорее начнём. Но прежде всего давайте вспомним, как называются числа при делении: делимое, делитель, частное.
А теперь посмотрите, какие примеры были заданы нашим математикам.

Обратите внимание на первый из них. В нем неизвестен делитель. Я предлагаю сделать к этому примеру рисунок. Так как в примере надо разделить число пятнадцать, нарисуем пятнадцать кружочков.

Но не в один ряд. Видите, что в примере в частном стоит число три, значит, надо разделить пятнадцать кружочков на несколько рядов так, чтобы было по три кружочка в каждом из них. Вот так: три, ещё три, снова три и ещё три. Вот наши кружочки по три в ряд, а всего рядов – один, два, три, четыре, пять. Пятнадцать кружочков разделено по три в ряд и получилось пять рядов. То есть неизвестное число равно пяти. Неизвестное число – это делитель. А как мы нашли неизвестный делитель? Делимое пятнадцать делили по три, то есть на частное.
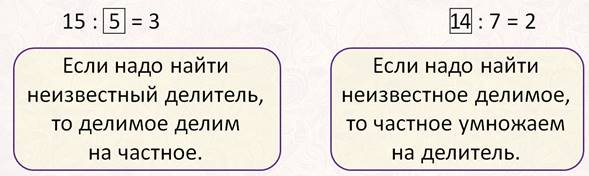
15 : 5 = 3
Выходит, что, если надо найти неизвестный делитель, надо делимое разделить на частное.
А как найти неизвестное делимое? Ведь во втором примере надо найти именно его. Давайте и к этому примеру сделаем рисунок. Пусть это будут не кружочки, а, например, треугольники.
На рисунке, иллюстрирующем пример, неизвестное количество треугольников должно разделиться на семь рядов, в каждом из которых должно получиться по два треугольника. Рисуем по два треугольника семь рядов, то есть семь раз.

И теперь мы видим, что треугольников четырнадцать. Получается, что наше неизвестное число, делимое, равно четырнадцати. А как мы получили это делимое. Взяли по два треугольника семь раз, то есть выполняли действие умножения.
2 × 7 = 14
Выходит, что, если надо найти неизвестное делимое, надо частное умножить на делитель. Или делитель умножить на частное.
Давайте проверим сделанные нами выводы. Сначала решим вот такой пример:
шестьдесят три разделить на девять равно. Вспомнили таблицу умножения и деления на девять? Конечно, равно семи. А теперь представьте себе, что в этом примере известны и делимое, и частное, но неизвестен делитель.
Как мы его найдём? Вспомним наш первый вывод: если надо найти неизвестный делитель, мы делимое делим на частное.
Проверяем вывод. Шестьдесят три делим на семь, получается девять. Да, вывод подтвердился.
А теперь попробуем найти делимое.
Вспоминаем наш второй вывод: если надо найти неизвестное делимое, мы частное умножаем на делитель.
Проверяем и этот вывод. Умножаем семь на девять. Получается шестьдесят три. И второй вывод тоже подтвердился. Значит, можно вывести правило:
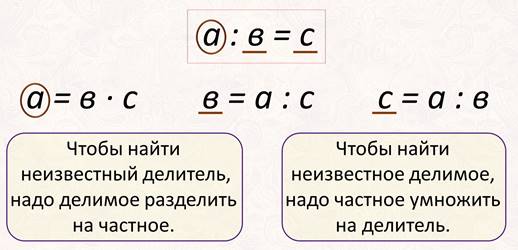
Чтобы найти неизвестный делитель, надо делимое разделить на частное.
Чтобы найти неизвестное делимое, надо частное умножить на делитель.
А для того, чтобы было легче запомнить эти правила, предлагаю вам посмотреть на эту формулу. а : в = с Делимое я обведу кружочком – его мы находим умножением, а делитель и частное – подчеркну. Их находим делением.
Ну, а теперь я предлагаю потренироваться и найти пропущенные числа в примерах.

Ну как, справились?
В примерах первой строчки надо было найти неизвестный делитель. Его мы находим делением – делимое делим на частное.

В примерах второй строчки надо было найти неизвестное делимое. Его мы находим умножением.
Ну вот и пришло время нам сегодня прощаться. Но правила, о которых я вам сегодня рассказал, обязательно постарайтесь запомнить. Они вам очень пригодятся при решении уравнений. Неизвестное делимое находим умножением, а делитель и частное – делением.
Чтобы найти неизвестный делитель, надо делимое разделить на частное.
Чтобы найти неизвестное делимое, надо частное умножить на делитель.
А я желаю вам получать только отличные отметки. До новых встреч, ребята!

 Получите свидетельство
Получите свидетельство Вход
Вход




 3047
3047

