Сегодня на уроке мы продолжим изучать десятичные дроби, а точнее научимся сравнивать их.
До этого мы с вами научились сравнивать натуральные числа и сравнивать дробные числа. Мы уже знаем, что числа могут быть равны, а могут быть и не равны, т.е. либо больше, либо меньше.
Давайте представим, что длина шоколадного батончика 8 см, это то же самое, что и 80 мм.

Мы знаем, что 1 см =  дм, значит 8
см =
дм, значит 8
см =  дм.
дм.

Отсюда видим, что если в конце десятичной дроби дописать нуль, или отбросить нуль, то получится дробь, равная данной.
Например

Мы рассмотрели с вами варианты равных дробей. А теперь давайте рассмотрим случаи, когда дроби не равны.
Задание
Сравним десятичные дроби: 3,56 и 4,23.

В этом примере мы сравнивали дроби, у которых разные целые части. А как поступить когда у дробей равные целые части, но разные дробные?
Запомните! Удобно сравнивать десятичные дроби, когда после запятой стоит одинаковое количество знаков.
Например
Сравним дроби: 4,23 и 4,191.

Чтобы сравнить две десятичные дроби, надо сначала уравнять у них число десятичных знаков, приписав, к одной из них справа нули, а потом, отбросив запятую, сравнить получившиеся натуральные числа.
Запишем алгоритм сравнения десятичных дробей:

Задание
Воспользуемся алгоритмом и сравним дроби: 5,336 и 5,63.

Десятичные дроби, как и обыкновенные дроби, можно изображать на координатном луче.
Например
Изобразим на координатном луче дробь 0,3.

Равные десятичные дроби изображаются на координатном луче одной и той же точкой.
Например
Отметим на координатном луче точки с координатами 0,8 и 0,80.

Меньшая десятичная дробь лежит на координатном луче левее большей. И наоборот, большая десятичная дробь лежит правее меньшей.
Итоги
Итак, сегодня на уроке мы научились сравнивать десятичные дроби и применили свои знания на примерах.

 Получите свидетельство
Получите свидетельство Вход
Вход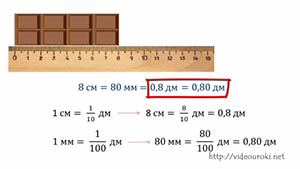



 0
0 2304
2304

