Напомним, что прямая, пересекающая плоскость, называется перпендикулярной плоскости, если она перпендикулярна каждой прямой, лежащей в этой плоскости.
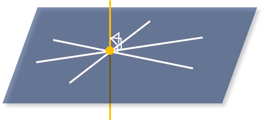
Теорема 1. Если одна из двух параллельных прямых перпендикулярна третьей прямой, то и другая прямая перпендикулярна этой прямой.

Теорема 2. Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости.
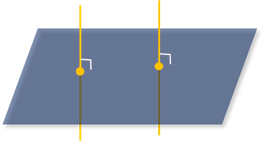
Теорема о параллельности прямых, перпендикулярных плоскости: если две прямые перпендикулярны одной плоскости, то они параллельны.
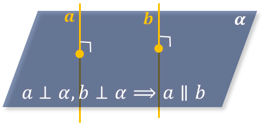
Признак перпендикулярности прямой и плоскости: если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости.
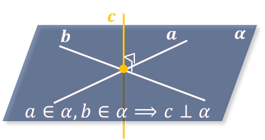
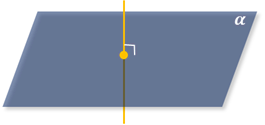
Теорема о плоскости, проходящей через данную точку и перпендикулярной данной прямой: через любую точку пространства проходит единственная плоскость, перпендикулярная данной прямой.
Теорема о прямой, проходящей через данную точку и перпендикулярной данной плоскости: через любую точку пространства проходит единственная прямая, перпендикулярная данной плоскости.
Также
напомним, что две плоскости называются перпендикулярными, если угол
между ними равен 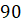 .
.
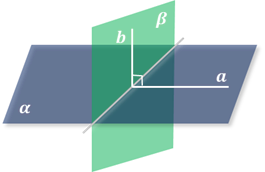
Признак перпендикулярности плоскостей: если одна из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Теорема 3. Прямая, лежащая в одной из двух перпендикулярных плоскостей и перпендикулярная прямой, по которой они пересекаются, перпендикулярна другой плоскости.
А теперь давайте рассмотрим следующий рисунок.
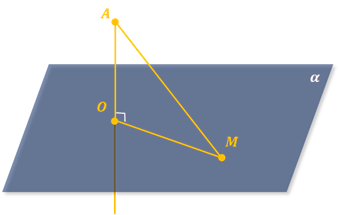
Здесь
точка 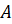 не
лежит на плоскости
не
лежит на плоскости 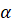 ,
отрезок
,
отрезок 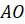 –
перпендикуляр, проведённый из точки
–
перпендикуляр, проведённый из точки 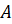 к
плоскости
к
плоскости 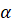 ,
точка
,
точка 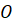 –
основание перпендикуляра, а точка
–
основание перпендикуляра, а точка 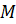 –
произвольная точка этой плоскости. Итак, наклонной, проведённой к данной
плоскости, называется прямая, пересекающая плоскость, но не перпендикулярная
ей. Точка пересечения наклонной и плоскости называется основанием наклонной.
–
произвольная точка этой плоскости. Итак, наклонной, проведённой к данной
плоскости, называется прямая, пересекающая плоскость, но не перпендикулярная
ей. Точка пересечения наклонной и плоскости называется основанием наклонной.
Проекцией точки на плоскость называется основание перпендикуляра, опущенного из данной точки на данную плоскость.
Проекцию прямой на плоскость задают проекции двух её точек на плоскость или точка пересечения прямой и плоскости и проекция одной из её точек.
Проекцией наклонной на плоскость называется прямая, состоящая из проекций всех точек наклонной на данную плоскость.
Перпендикуляр и проекция меньше наклонной, так как катет меньше гипотенузы.
Углом между наклонной и плоскостью называется угол между наклонной и её проекцией.
Углом
между прямой и плоскостью называется угол между прямой и её
проекцией на эту плоскость (если прямая параллельна плоскости, то этот угол
равен 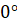 ,
если перпендикулярна –
,
если перпендикулярна – 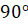 ).
).
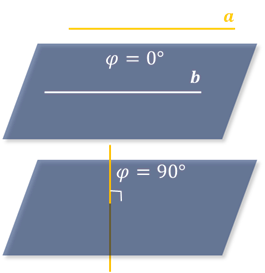
Вспомним теорему о трёх перпендикулярах: прямая, проведённая в плоскости и перпендикулярная проекции наклонной на эту плоскость, перпендикулярна и самой наклонной.
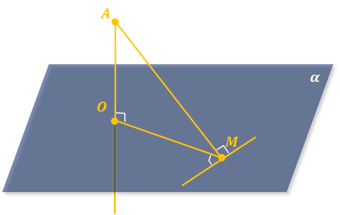
Прямая, проведённая в плоскости и перпендикулярная наклонной, перпендикулярна и её проекции на эту плоскость.
Теорема о наклонных, проведённых из одной точки: если из одной точки к плоскости проведены перпендикуляр и несколько наклонных, то меньшей наклонной соответствует меньшая проекция, большей – большая, равным наклонным соответствуют равные проекции и наоборот.
Расстоянием от точки до плоскости называется длина перпендикуляра, проведённого из этой точки к данной плоскости.
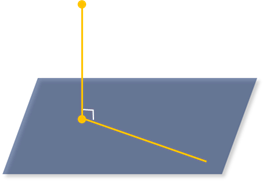
Расстоянием между параллельными плоскостями называется расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости.
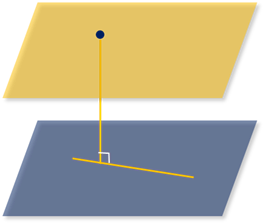
Расстоянием между прямой и параллельной ей плоскостью называется расстояние от произвольной точки прямой до плоскости.
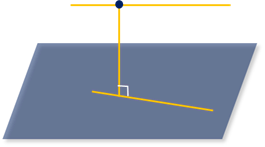
Расстоянием между скрещивающимися прямыми называется расстояние от одной из скрещивающихся прямых до плоскости, проходящей через другую прямую и параллельной первой прямой.

Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.
Задача
первая. Отрезок 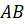 не
имеет общих точек с плоскостью
не
имеет общих точек с плоскостью 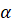 .
Через точки
.
Через точки 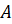 и
и
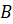 проведены
прямые, перпендикулярные плоскости и пересекающие её в точках
проведены
прямые, перпендикулярные плоскости и пересекающие её в точках 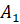 и
и
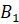 соответственно.
Вычислите длину отрезка
соответственно.
Вычислите длину отрезка 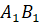 ,
если
,
если 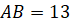 см,
см,
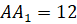 см
и
см
и 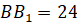 см.
см.
Решение.


Задача
вторая. Периметр ромба 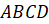 равен
равен
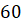 см,
диагональ
см,
диагональ 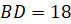 см.
Из вершины
см.
Из вершины 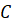 восстановлен
перпендикуляр
восстановлен
перпендикуляр 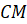 ,
равный
,
равный 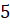 см.
Найдите расстояние от точки
см.
Найдите расстояние от точки 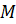 до
прямой
до
прямой 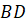 .
.
Решение.
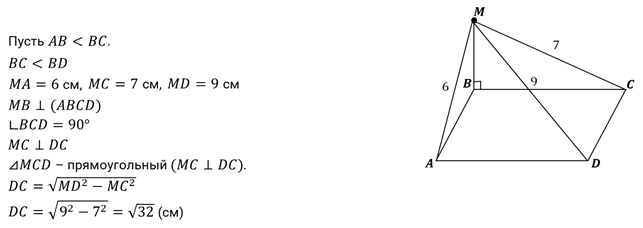
Задача
третья. Из вершины 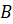 прямоугольника
прямоугольника
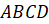 восстановлен
перпендикуляр
восстановлен
перпендикуляр 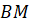 к
плоскости прямоугольника. Расстояния от точки
к
плоскости прямоугольника. Расстояния от точки 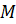 до
остальных вершин прямоугольника равны
до
остальных вершин прямоугольника равны 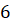 см,
см,
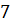 см
и
см
и 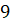 см.
Найдите длину перпендикуляра
см.
Найдите длину перпендикуляра 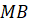 .
.
Решение.

Задача
четвёртая. Дан куб. Найдите расстояние между прямыми 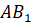 и
и
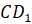 ,
если длина ребра куба равна
,
если длина ребра куба равна 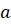 .
.
Решение.

Задача
пятая. 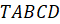 –
четырёхугольная пирамида, основание которой – квадрат
–
четырёхугольная пирамида, основание которой – квадрат 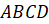 .
Боковое ребро
.
Боковое ребро 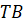 перпендикулярно
плоскости основания, а точка
перпендикулярно
плоскости основания, а точка 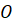 –
середина ребра
–
середина ребра 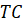 .
Найдите площадь сечения пирамиды плоскостью, проходящей через прямую
.
Найдите площадь сечения пирамиды плоскостью, проходящей через прямую 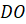 и
перпендикулярной плоскости основания, если
и
перпендикулярной плоскости основания, если 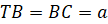 .
.
Решение.



 Получите свидетельство
Получите свидетельство Вход
Вход




 8014
8014