Напомним, что в стереометрии основными фигурами являются точки, прямые и плоскости.
Теперь давайте вспомним три основные аксиомы, используемые в стереометрии.
Первая аксиома: через любые три точки, не лежащие на одной прямой, проходит единственная плоскость.

Вторая аксиома: если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.

Третья аксиома: если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

Из аксиом вытекают следующие следствия.
Через прямую и не лежащую на ней точку проходит единственная плоскость.

Через две пересекающиеся прямые проходит единственная плоскость.

А теперь поговорим о параллельности прямых, прямой и плоскости, плоскостей.
Итак, две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Теорема 1. Через любую точку пространства, не лежащую на данной прямой, проходит единственная прямая, параллельная данной прямой.

Теорема 2. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

Признак параллельности прямых: если две прямые параллельны третьей прямой, то они параллельны между собой.
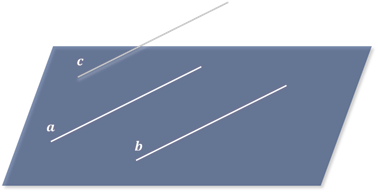
В пространстве возможны три случая взаимного расположения прямой и плоскости.
Прямая лежит в плоскости (каждая точка прямой лежит в плоскости).

Прямая и плоскость пересекаются (имеют единственную общую точку).

Прямая и плоскость не имеют ни одной общей точки.

Прямая и плоскость называются параллельными, если они не имеют общих точек.

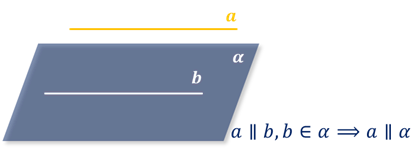
Признак параллельности прямой и плоскости: если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.
Теорема 3.Если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту другую плоскость, то линия пересечения плоскостей параллельна данной прямой.
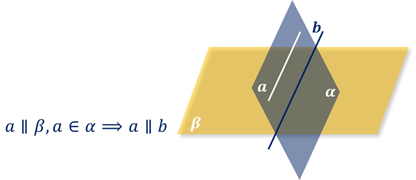
Две плоскости называются параллельными, если они не пересекаются.

Признак параллельности плоскостей: если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
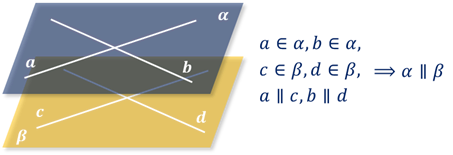
Свойства параллельных плоскостей.
Если две параллельные плоскости пересечены третьей, то прямые их пересечения параллельны между собой.
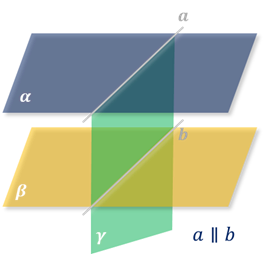
Отрезки параллельных прямых, расположенные между параллельными плоскостями, равны.
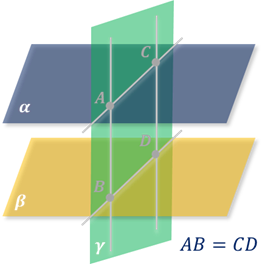
Через точку, не лежащую в данной плоскости, проходит единственная плоскость, параллельная данной.

Также напомним, что в пространстве возможны три случая взаимного расположения двух прямых.
Прямые пересекаются (имеют одну общую точку).

Прямые параллельны (лежат в одной плоскости и не пересекаются).

Прямые скрещиваются (не существует плоскости, в которой они обе лежат).

Две прямые называются скрещивающимися, если не существует плоскости, в которой они обе лежат.
Признак скрещивающихся прямых: если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не принадлежащей первой прямой, то эти прямые скрещиваются.
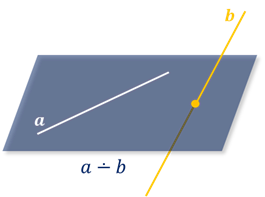
Теорема 4. Через каждую из двух скрещивающихся прямых проходит единственная плоскость, параллельная другой прямой.
Угол между скрещивающимися прямыми определяется как угол между параллельными им прямыми, проходящими через одну точку.
Общим перпендикуляром двух скрещивающихся прямых называется отрезок, концы которого лежат на этих прямых, перпендикулярный к ним (такой отрезок существует и притом только один).
Расстоянием между двумя скрещивающимися прямыми называется длина их общего перпендикуляра (оно же является и расстоянием между параллельными плоскостями, содержащими эти прямые).
Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.
Задача
первая. Даны параллельные прямые 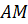 и
и
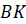 ,
точки
,
точки 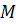 ,
,
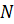 ,
,
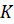 принадлежат
плоскости
принадлежат
плоскости 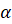 .
Найдите длину
.
Найдите длину 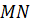 ,
если
,
если 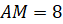 ,
,
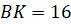 ,
,
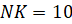 .
.
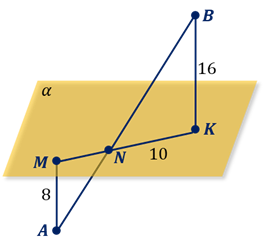
Решение.

Задача
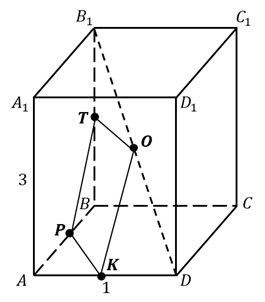
вторая. Основанием прямоугольного параллелепипеда служит
квадрат, длина стороны которого 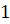 см,
а длина бокового ребра параллелепипеда равна
см,
а длина бокового ребра параллелепипеда равна 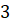 см.
Точки
см.
Точки 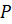 ,
,
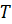 ,
,
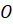 и
и
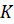 являются
серединами отрезков
являются
серединами отрезков 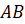 ,
,
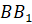 ,
,
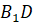 и
и
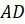 соответственно.
Вычислите периметр четырёхугольника
соответственно.
Вычислите периметр четырёхугольника 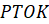 .
.
Решение.
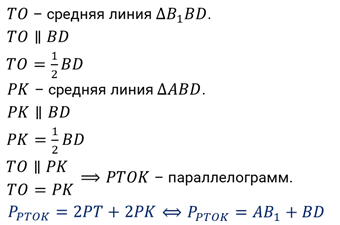
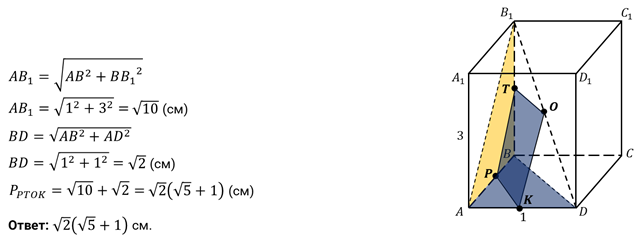
Задача
третья. Точки 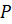 ,
,
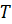 и
и
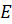 –
соответственно середины рёбер
–
соответственно середины рёбер 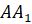 ,
,
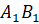 и
и
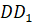 параллелепипеда
параллелепипеда
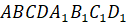 .
Постройте сечение параллелепипеда плоскостью, проходящей через точки
.
Постройте сечение параллелепипеда плоскостью, проходящей через точки 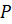 ,
,
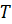 и
и
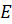 .
Какая фигура получится в сечении?
.
Какая фигура получится в сечении?
Решение.

Задача
четвёртая. Дан куб. Найдите угол между прямыми 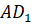 и
и
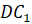 .
.
Решение.

Задача
пятая. Треугольник 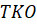 –
сечение правильной треугольной пирамиды
–
сечение правильной треугольной пирамиды 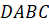 плоскостью,
проходящей через точку
плоскостью,
проходящей через точку 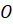 ,
причём
,
причём 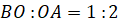 ,
и параллельной плоскости
,
и параллельной плоскости 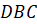 .
Вычислите периметр треугольника
.
Вычислите периметр треугольника 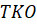 ,
если длина стороны основания пирамиды равна
,
если длина стороны основания пирамиды равна 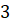 см,
а длина бокового ребра –
см,
а длина бокового ребра – 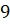 см.
см.
Решение.




 Получите свидетельство
Получите свидетельство Вход
Вход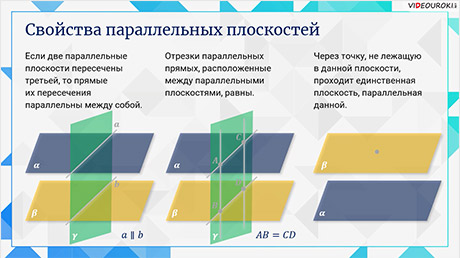




 13985
13985





