Напомним, что площадь многоугольника – это величина части плоскости, которую занимает многоугольник. За единицу измерения площади принимается квадрат, сторона которого равна единице измерения отрезков. Площадь многоугольника выражается положительным числом, которое показывает, сколько раз единица измерения и её части укладываются в данном многоугольнике.
Вспомним некоторые свойства площадей.
1. Равные многоугольники имеют равные площади.
2. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
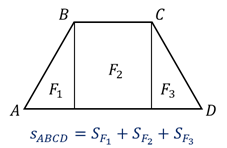
3. Площадь квадрата равна квадрату его стороны, то есть если
сторона квадрата при выбранной единице измерения отрезков выражается числом 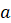 , то площадь этого квадрата выражается числом
, то площадь этого квадрата выражается числом 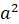 .
.
Первое и второе свойства называют основными свойствами площадей.
Теперь вспомним, что площадь прямоугольника равна произведению длин его смежных сторон.

Прежде чем вспомнить, чему равна площадь параллелограмма, напомним, что высотой параллелограмма, проведённой к стороне, называется перпендикуляр (или его длина), проведённый из любой точки противоположной стороны к прямой, содержащей эту сторону. Площадь параллелограмма равна произведению длины стороны на высоту, проведённую к ней.

Площадь треугольника. Напомним, что высотой треугольника называется перпендикуляр (или длина перпендикуляра), проведённый из вершины треугольника к прямой, содержащей противоположную сторону треугольника. Площадь треугольника равна половине произведения длины стороны на высоту, проведённую к ней.

Площадь прямоугольного треугольника равна половине произведения длин его катетов.

Если высота одного треугольника равна высоте другого треугольника, то их площади относятся как длины сторон, к которым проведены высоты.
Вспомним теорему об отношении площадей треугольников, имеющих по равному углу. Итак, если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения длин сторон, заключающих равные углы.

Площадь трапеции. Напомним, что высотой трапеции называется перпендикуляр, опущенный из любой точки одного из оснований на другое основание или его продолжение. Площадь трапеции равна произведению полусуммы длин её оснований на высоту.

Площадь ромба равна половине произведения длин диагоналей.

Площадь круга радиуса  можно вычислить по формуле
можно вычислить по формуле  .
.
Сектором называется часть круга, ограниченная дугой окружности и двумя радиусами, соединяющими концы дуги с центром круга.
Дуга, которая ограничивает сектор, называется дугой сектора.
Площадь сектора,
ограниченная дугой, градусная мера которой равна  градусов, можно найти по формуле
градусов, можно найти по формуле  .
.

Мы с вами повторили основные моменты, а теперь давайте перейдём к практической части занятия.
Задача
первая. Найдите периметр прямоугольника  ,
если его площадь равна
,
если его площадь равна  см²,
а сторона
см²,
а сторона  в
два раза больше стороны
в
два раза больше стороны  .
.
Решение.

Задача
вторая. Длина стороны  параллелограмма
параллелограмма
 равна
равна
 см.
Найдите высоту, проведённую к этой стороне, если площадь параллелограмма равна
см.
Найдите высоту, проведённую к этой стороне, если площадь параллелограмма равна  см².
см².
Решение.

Задача
третья. В равнобедренном треугольнике  боковые
стороны
боковые
стороны  и
и
 равны
равны
 см,
основание
см,
основание  равно
равно
 см.
Найдите площадь треугольника.
см.
Найдите площадь треугольника.
Решение.

Задача
четвёртая. Медиана  прямоугольного
треугольника
прямоугольного
треугольника  ,
проведённая к гипотенузе
,
проведённая к гипотенузе  ,
равна
,
равна  см.
Проекция
см.
Проекция  медианы
медианы
 на
гипотенузу
на
гипотенузу  равна
равна
 см.
Найдите площадь треугольника
см.
Найдите площадь треугольника  .
.
Решение.

Задача
пятая. Диагонали ромба  относятся
как
относятся
как  .
Найдите площадь ромба, если его периметр равен
.
Найдите площадь ромба, если его периметр равен  см.
см.
Решение.

Задача
шестая. У равнобедренной трапеции  основание
основание
 равно
равно
 см,
основание
см,
основание  равно
равно
 см,
боковая сторона равна
см,
боковая сторона равна  см.
Найдите площадь трапеции.
см.
Найдите площадь трапеции.
Решение.

Задача
седьмая. Площадь квадрата равна  см².
Найдите площадь части квадрата, лежащей вне вписанной в него окружности.
см².
Найдите площадь части квадрата, лежащей вне вписанной в него окружности.
Решение.

Задача
восьмая. Длина окружности, ограничивающей круг, равна  см.
Градусная мера вписанного в окружность
см.
Градусная мера вписанного в окружность  равна
равна
 .
Найдите площадь сектора, ограниченного дугой, на которую опирается вписанный
угол, и радиусами, соединяющими концы этой дуги с центром круга.
.
Найдите площадь сектора, ограниченного дугой, на которую опирается вписанный
угол, и радиусами, соединяющими концы этой дуги с центром круга.
Решение.


 Получите свидетельство
Получите свидетельство Вход
Вход




 2739
2739



