Сегодня на уроке мы вспомним, что называют случайными величинами. Узнаем, что называют генеральной совокупностью и выборкой. Выясним, какую выборку называют репрезентативной. Узнаем, что является модой, медианой и средним арифметическим. Поговорим о математическом ожидании.
Начнём с примеров. Возьмём девочек одного класса. Их можно сравнивать по возрасту, росту, весу. Российские монеты можно сравнивать по номиналу, весу, диаметру. Книги, стоящие на полке, можно сравнивать по высоте, цвету и количеству страниц. Получается, что однотипные объекты можно сравнивать по общим параметрам, которые присущи этим объектам. Каждый из названных параметров может принимать определённые числовые значения.
В статистике исследуют различные совокупности данных – числовых значений случайных величин с учётом частот, с которыми они встречаются в совокупности.
Совокупность всех данных называют генеральной совокупностью, а любую выбранную из неё часть – выборкой.
Выборку называют репрезентативной, если в ней присутствуют те и только те значения случайной величины, что и в генеральной совокупности, причём частоты имеющихся в ней данных находятся практически в тех же отношениях, что и в генеральной совокупности. Слово «репрезентативный» произошло от французского слова, которое переводится как «представительный».
Рассмотрим это на примере.

В данной таблице представлено распределение значений случайной величины X по частотам M. Совокупность всех значений этой величины принята за генеральную совокупность.
Тогда выборку из этой совокупности, распределение которой представлено в следующей таблице, следует считать репрезентативной, так как частоты имеющихся в ней данных находятся в тех же отношениях, что и в генеральной совокупности, и в выборке присутствуют те и только те значения случайной величины X, которые присутствуют в генеральной совокупности.

А теперь посмотрите на выборки, которые представлены в следующих двух таблицах.

Эти выборки не являются репрезентативными. А всё потому, что в первой таблице значения случайной величины отличаются от значений случайной величины в генеральной совокупности. Во второй таблице частоты имеющихся в ней данных очевидно находятся не в тех отношениях, что в генеральной совокупности.
Отметим, что совокупность данных иногда бывает полезно охарактеризовать одним числом, которое называют мерой центральной тенденции числовых значений её элементов. К таким характеристикам относятся мода, медиана и среднее. Поговорим про каждое из них.
Итак, мода – это значение случайной величины, имеющее
наибольшую частоту в рассматриваемой выборке. Обозначается мода вот таким
образом  .
.
Например, мода выборки  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  равна
равна
 , так
как число
, так
как число  встречается
в данной выборке чаще остальных значений (
встречается
в данной выборке чаще остальных значений ( раза).
Теперь посмотрите на следующую выборку
раза).
Теперь посмотрите на следующую выборку  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  . В этой выборке число
. В этой выборке число  встречается
встречается
 раза
и число
раза
и число  тоже
встречается
тоже
встречается  раза.
Остальные значения в этой выборке встречаются только
раза.
Остальные значения в этой выборке встречаются только  раз.
Поэтому данная выборка имеет две моды:
раз.
Поэтому данная выборка имеет две моды:  ,
,  .
.
Медиана – это число (значение случайной величины), разделяющее упорядоченную выборку на две равные по количеству данных части.
Обозначается медиана вот таким образом  .
.
Важно обратить внимание, что если в упорядоченной выборке нечётное количество данных, то медиана равна серединному из них. Если в упорядоченной выборке чётное количество данных, то медиана равна среднему арифметическому двух серединных чисел.
Давайте найдём медиану выборки значений случайной величины:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  . В
первую очередь мы должны расположить элементы выборки в порядке возрастания:
. В
первую очередь мы должны расположить элементы выборки в порядке возрастания:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
Обратите внимание, что количество данных равно
.
Обратите внимание, что количество данных равно  , то
есть нечётно. Слева и справа от числа
, то
есть нечётно. Слева и справа от числа  находятся
по четыре элемента, то есть
находятся
по четыре элемента, то есть  –
серединное число выборки, следовательно,
–
серединное число выборки, следовательно,  .
.
Найдём медиану ещё одной выборки:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  . Расположим
её элементы в порядке возрастания:
. Расположим
её элементы в порядке возрастания:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
Количество данных равно
.
Количество данных равно  , то
есть чётно. Серединные данные выборки:
, то
есть чётно. Серединные данные выборки:  и
и  .
Поэтому
.
Поэтому  .
.
Среднее (или среднее арифметическое) выборки – это число, равное отношению суммы всех чисел выборки к их количеству.
Если рассматривается совокупность значений случайной величины  , то
её среднее обозначают
, то
её среднее обозначают  .
.
Давайте найдём среднее выборки значений случайной величины  ,
распределение которых по частотам представлено в следующей таблице.
,
распределение которых по частотам представлено в следующей таблице.


Одной из наиболее распространённых характеристик выборки значений случайной величины, чьё распределение по вероятностям известно, является математическое ожидание.
Пусть в следующей таблице задано распределение значений некоторой
случайной величины  по
вероятностям P.
по
вероятностям P.

Тогда число

называют математическим ожиданием (или средним значением) случайной величины икс.
Пусть случайная величина  –
сумма чисел, выпавших при бросании двух игральных костей. На одном из
предыдущих занятий мы с вами составили таблицу распределения значений этой
случайной величины по их вероятностям. Сейчас мы можем найти её математическое
ожидание, то есть
–
сумма чисел, выпавших при бросании двух игральных костей. На одном из
предыдущих занятий мы с вами составили таблицу распределения значений этой
случайной величины по их вероятностям. Сейчас мы можем найти её математическое
ожидание, то есть  .
.

Отметим, что математическое ожидание широко применяется в играх.
Например, предположим, что в некоторой игре с двумя игроками
первый игрок может выиграть  ,
,  , …,
, …,  рублей.
Отметим, что среди этих чисел могут быть отрицательные (в случае проигрыша) и
рублей.
Отметим, что среди этих чисел могут быть отрицательные (в случае проигрыша) и  .
Суммарный выигрыш двух игроков всегда равен
.
Суммарный выигрыш двух игроков всегда равен  . При
этом вероятность того, что первый игрок выиграет
. При
этом вероятность того, что первый игрок выиграет  рублей,
равна
рублей,
равна  .
Тогда средний выигрыш первого игрока будет равен
.
Тогда средний выигрыш первого игрока будет равен  .
.
Если получится, что  (то
есть данная сумма равна
(то
есть данная сумма равна  ), то
игра называется справедливой.
), то
игра называется справедливой.
Если  , то
игра называется выгодной для первого игрока.
, то
игра называется выгодной для первого игрока.
Если же  , то
игра называется невыгодной для первого игрока.
, то
игра называется невыгодной для первого игрока.
А сейчас мы с вами выполним задание. Найдите моду, медиану и среднее значение выборки:
1)  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ;
;
2)  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Решение.


 Получите свидетельство
Получите свидетельство Вход
Вход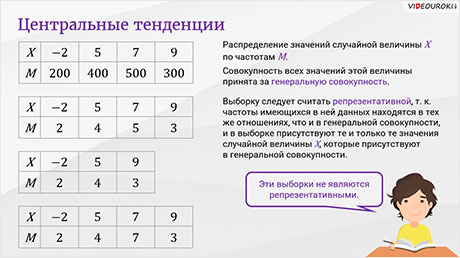




 3363
3363

