Сегодня на уроке мы вспомним, что называют относительной частотой события.
Напомним, чем занимается статистика. Выясним, какие величины называют случайными. Узнаем, какие величины называют дискретными, а какие – непрерывными.
Прежде, чем приступить к рассмотрению новой темы, вспомним, что относительной
частотой события  в
данной серии испытаний называют отношение числа испытаний
в
данной серии испытаний называют отношение числа испытаний  , в
которых это событие произошло, к числу всех проведённых испытаний
, в
которых это событие произошло, к числу всех проведённых испытаний  . При
этом число
. При
этом число  называют
частотой события
называют
частотой события  . Относительную
частоту события
. Относительную
частоту события  обозначают
обозначают
 .
.
Тогда по определению  .
.
Сегодня на занятии мы перейдём к изучению раздела математики, который называют статистикой.
Статистика – это наука, которая занимается получением, обработкой и анализом количественных данных о разнообразных массовых явлениях, происходящих в обществе и природе.
Можно сказать, что статистика занимается сбором, представлением (в виде таблиц, графиков, диаграмм) и анализом информации о различных случайных величинах.
Случайными величинами называют такие величины, которые в ходе наблюдений или испытаний могут принимать различные значения.
Можно говорить, что величину называют случайной, если она может принимать заранее неизвестные числовые значения, зависящие от случайных обстоятельств. Примерами являются число попаданий при трёх выстрелах; число вызовов, поступающих на телефонную станцию за сутки; число выпавших решек при бросании монеты.
Сумма чисел, выпадающая при бросании двух игральных костей, также
является случайной величиной. Обозначим её –  .
Отметим, что, как правило, случайные величины обозначают
.
Отметим, что, как правило, случайные величины обозначают  ,
,  ,
,  .
.
Случайная величина  может
принимать значения:
может
принимать значения:  ,
,  ,
,  , …,
, …,  . Каждое
из значений является суммой чисел, которые выпадают при бросании двух игральных
костей.
. Каждое
из значений является суммой чисел, которые выпадают при бросании двух игральных
костей.
Сейчас вы видите таблицу, в которой указаны возможные суммы, выпадающие при бросании двух игральных костей.

Ниже давайте составим таблицу, в которой покажем распределение
значений случайной величины X по их вероятностям P. Каждой из сумм ( ,
,  ,
,  , …,
, …,  )
поставим в соответствие вероятность, с которой она может появиться в результате
одного испытания, то есть одного бросания двух игральных костей.
)
поставим в соответствие вероятность, с которой она может появиться в результате
одного испытания, то есть одного бросания двух игральных костей.

Таким образом, мы показали распределение значений случайной
величины  по их
вероятностям. Иногда для наглядности это может быть изображено, например, в
виде линейной или столбчатой диаграммы.
по их
вероятностям. Иногда для наглядности это может быть изображено, например, в
виде линейной или столбчатой диаграммы.
Сумма вероятностей  всех
значений величины
всех
значений величины  ,
которые записаны во второй строке таблицы равна 1, как сумма вероятностей всех
элементарных исходов испытания с нахождением суммы очков при одном бросании
двух игральных костей.
,
которые записаны во второй строке таблицы равна 1, как сумма вероятностей всех
элементарных исходов испытания с нахождением суммы очков при одном бросании
двух игральных костей.

Посмотрите на знак, с помощью которого мы записали сумму значений вероятностей.
Этот знак был введён Леонардом Эйлером. Он используется для записи суммы значений некоторой величины.
Вообще, таблицы распределения значений случайной величины составляются по результатам теоретических расчётов вероятностей. На практике часто после проведения реальных испытаний составляются таблицы распределения значений случайных величин по частотам (или относительным частотам). Для наглядности распределение данных представляют в виде диаграммы или полигона частот (полигона относительных частот).
С диаграммами вы уже знакомы. Вы знаете, что диаграмма – это графическое изображение, наглядно показывающее соотношение между различными величинами. Полигон (или его ещё называют графиком) также используют для наглядного изображения распределения данных, полученных в результате статистического исследования.
Давайте решим задачу. В результате эксперимента получены следующие значения случайных величин:
 .
.
Представьте эти данные с помощью таблицы распределения по частотам и относительным частотам и с помощью полигона частот.
Решение. В первую очередь имеющиеся данные (значения случайной величины) представим в виде таблицы распределения по частотам и относительным частотам.

Теперь построим полигон частот. Для этого мы на координатной плоскости на оси абсцисс отметим значения случайной величины, а на оси ординат – значения частот. Отметим точки с соответствующими координатами. Затем последовательно соединив эти точки отрезками, получим ломаную, которую является полигоном частот.

Рассмотренные выше случайные величины принимали изолированные друг от друга значения. Такие величины называют дискретными, что в переводе с латинского означает «раздельный, прерывистый».
Если случайная величина принимает любое значение из некоторого промежутка, то такую величину называют непрерывной. Например, расстояние от точки попадания пули до центра мишени. Множество значений этой величины – некоторый непрерывный отрезок числовой прямой.
А сейчас выполним задание. Составьте таблицу распределения по частотам значений случайной величины X – цифр, встречающихся в выборке следующих телефонных номеров:
 .
.
Решение.

И выполним ещё одно задание. Постройте полигон частот значений случайной величины X, распределение которой представлено в следующей таблице.

Чтобы выполнить это задание, мы на координатной плоскости на оси абсцисс отметим значения случайной величины, а на оси ординат – значения частот. Отметим точки с соответствующими координатами. Затем, последовательно соединив эти точки отрезками, получим ломаную, которую является полигоном частот.


 Получите свидетельство
Получите свидетельство Вход
Вход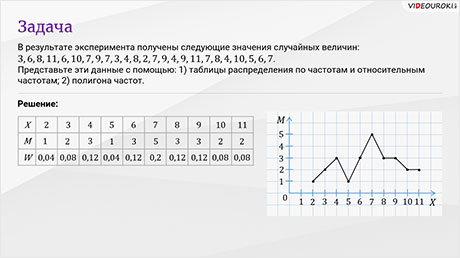




 4633
4633

