Меры разброса

Сегодня на уроке мы вспомним, что является модой, медианой и средним арифметическим выборки. Узнаем, что называется размахом выборки. Выясним, что называют отклонением от среднего. Познакомимся с величиной, которую называют дисперсией. Узнаем, что называют средним квадратичным отклонением.

Прежде, чем приступить к рассмотрению новой темы, давайте вспомним, что совокупность данных иногда бывает полезно оценить одним числом – мерой центральной тенденции числовых значений её элементов. К таким характеристикам относятся мода, медиана и среднее.

Итак, мода – это значение случайной величины, имеющее наибольшую частоту в рассматриваемой выборке.

Медиана – это число (значение случайной величины), разделяющее упорядоченную выборку на две равные по количеству данных части.

При этом если в упорядоченной выборке нечётное количество данных, то медиана равна серединному из них. Если в упорядоченной выборке чётное количество данных, то медиана равна среднему арифметическому двух серединных чисел.

Среднее (или среднее арифметическое) выборки – это число, равное отношению суммы всех чисел выборки к их количеству. Если рассматривается совокупность значений случайной величины , то её среднее обозначают .

Отметим, что не каждую выборку имеет смысл оценивать с помощью центральных тенденций.

Так, например, посмотрите на следующую выборку , , 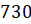,  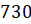Это выборка выигрышей (в рублях) четырёх человек. Здесь мода равна 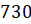. Медиана также равна 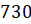. Среднее равно .

Очевидно, что ни мода, ни медиана, ни среднее не могут выступать в роли единой объективной характеристики данной выборки. Это объясняется тем, что наименьшие значения этой выборки существенно отличаются от наибольшего. А вот разность наибольшего и наименьшего значений соизмерима с наибольшим значением ().

Сформулируем определение. Разность наибольшего и наименьшего значений случайной величины выборки называется её размахом и обозначается буквой R.

Для рассматриваемой выборки размах равен разности  и , то есть равен .

Размах показывает, насколько велик разброс значений случайной величины в выборке. Однако, зная размах выборки, невозможно охарактеризовать отличие её элементов друг от друга, отличие каждого элемента от среднего значения.

А как сравнить две выборки, которые имеют одинаковые размахи и одинаковые средние значения?

Давайте рассмотрим пример. На место столяра претендуют двое рабочих. Для каждого из них установили испытательный срок, в течение которого они должны изготавливать одинаковые стулья из дерева. В следующей таблице приведены результаты претендентов.

Каждый из рабочих за пять дней изготовил  деталей. Следовательно, средняя производительность труда за день у обоих рабочих одинаковая и равна  стульев в день.

Моды у предложенных совокупностей отсутствуют. Чтобы найти медианы, расположим значения в порядке возрастания.

, , , , ; , , , , .

Количество данных в обоих случаях нечётно. Слева и справа от числа  находятся по два элемента. Получается, что медианы одинаковые ( и ).

В качестве критерия сравнения совокупностей в данном случае может выступать стабильность производительности труда. Её можно оценить с помощью отклонений от среднего значения элементов совокупности.

Давайте сформулируем определение. Отклонением от среднего называют разность между рассматриваемым значением случайной величины и средним значением выборки.

Например, если значение , а значение , то отклонение  от среднего равно .

Отклонение от среднего может быть как положительным, так и отрицательным.

Найдём отклонение от среднего и внесём найденные значения в таблицу.

Покажем на нашем примере, что сумма отклонений всех значений выборки от среднего значения равна .

, .

Поэтому характеристикой стабильности элементов совокупности может служить сумма квадратов отклонений от среднего.

Давайте найдём квадраты отклонений от среднего и суммы квадратов отклонений.

Видим, что у второго рабочего сумма квадратов отклонений от среднего больше, чем у первого, то есть можно записать неравенство .

На практике это означает, что второй рабочий имеет нестабильную производительность труда: в какие-то дни он работает не в полную силу, а какие-то навёрстывает упущенное, а это всегда сказывается на качестве продукции.

Получается, что работодатель захочет взять на место столяра первого рабочего, ведь у первого рабочего сумма квадратов отклонений от средней производительности меньше.

В рассмотренном примере рабочие работали одинаковое количество дней. Если бы рабочие работали разное количество дней и производили в среднем за день одинаковое число деталей, то стабильность работы каждого из них можно было бы оценить по величине среднего арифметического квадратов отклонений. Такая величина называется дисперсией, что в переводе с латинского означает «рассеяние», и обозначается буквой .

Для случайной величины , принимающей  различных значений и имеющей среднее значение , дисперсия находится по формуле

Давайте решим задачу. Два столяра изготавливали одинаковые стулья из дерева. При этом первый столяр трудился полную рабочую неделю, а второй –  дня. Сведения об их дневной выработке представлены в таблице. Сравните стабильность работы столяров.

Итак, найдём средние значения выборок данных величин X и Y.

, .

Таким образом, мы получили, что найденные значения равны.

Далее найдём отклонения от среднего для всех значений величин X и Y.

Затем найдём квадраты отклонений от среднего. Найдём сумму квадратов отклонений от среднего всех значений величин X и Y.

Теперь найдём дисперсию совокупности значений случайной величины X, то есть среднее арифметическое квадратов отклонений.

Найдём дисперсию совокупности значений случайной величины Y.

Таким образом мы получили, что .

Следовательно, второй столяр работает стабильнее первого.

Отметим, что если значения 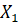, , …,  случайной величины  повторяются с частотами , , …,  соответственно, то дисперсию величины  можно вычислить по формуле

,

 где .

Используя знак суммы Ʃ, данную формулу можно записать более компактно.

, где .

Пусть величина  имеет некоторую размерность (например, миллиметры). Тогда её среднее значение  и отклонение от среднего  имеют ту же размерность, что и сама величина (в миллиметрах). А вот квадрат отклонения  и дисперсия   имеют размерности квадрата этой величины (в квадратных миллиметрах).

Для оценки степени отклонения от среднего значения удобно иметь дело с величиной той же размерности, что и сама величина . С этой целью используются значения .

Сформулируем определение. Корень квадратный из дисперсии называют средним квадратичным отклонением и обозначают , то есть .

Давайте найдём среднее квадратичное отклонение от среднего значения выборки:

 см,  см,  см,  см,  см.

Вообще, дисперсию и среднее квадратичное отклонение в статистике называют также мерами рассеивания значений случайной величины около среднего значения.