Вспомним формулы
сложения для синуса: 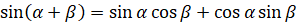 ,
, 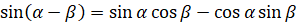 ; косинуса:
; косинуса: 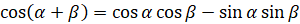 ,
, 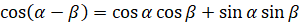 . Эти формулы мы будем использовать при
доказательстве формул суммы и разности синусов и формул суммы и
разности косинусов.
. Эти формулы мы будем использовать при
доказательстве формул суммы и разности синусов и формул суммы и
разности косинусов.
Итак, докажем, что 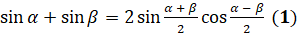 .
.
Обозначим 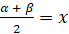 ,
, 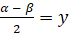 . Тогда
. Тогда 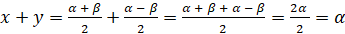 , а
, а 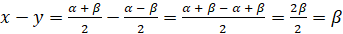 . Таким образом, можем записать,
. Таким образом, можем записать, 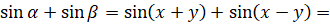 [
[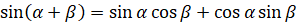 ,
, 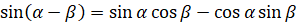 ]
] 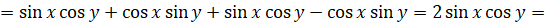
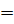 [вернёмся к замене]
[вернёмся к замене] 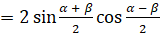 . Формула
. Формула 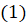 доказана.
доказана.
Читается эта формула так: сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус их полуразности.
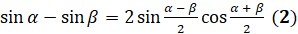 . Эта формула получается из формулы
. Эта формула получается из формулы 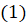 заменой
заменой 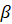 на
на 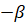 :
: 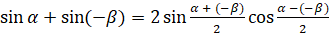 . Выполним преобразования и получим:
. Выполним преобразования и получим: 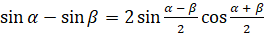 .
.
Читается эта формула так: разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус их полусуммы.
Теперь докажем формулу суммы косинусов: 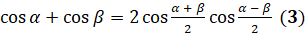 .
.
Обозначим 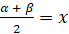 ,
, 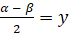 . Тогда
. Тогда 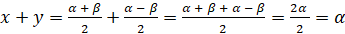 , а
, а 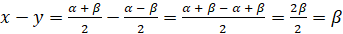 .
.
Поэтому 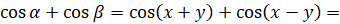 [
[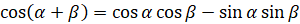 ,
, 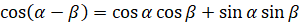 ]
] 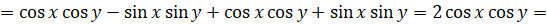 [вернёмся к замене]
[вернёмся к замене] 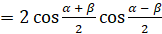 . Таким образом, формула
. Таким образом, формула 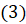 доказана. Читается формула так: сумма косинусов
двух углов равна удвоенному произведению косинуса полусуммы этих углов на
косинус их полуразности.
доказана. Читается формула так: сумма косинусов
двух углов равна удвоенному произведению косинуса полусуммы этих углов на
косинус их полуразности.
И нам осталось рассмотреть формулу разности косинусов.
Она получается из формулы 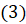 заменой
заменой 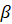 на
на 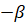 ? Нет. Формула разности косинусов доказывается так же, как формулы
? Нет. Формула разности косинусов доказывается так же, как формулы 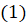 и
и 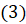 .
.
Докажем, что 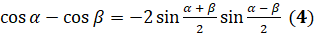 .
.
Обозначим 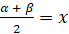 ,
, 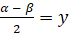 . Тогда
. Тогда 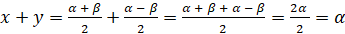 , а
, а 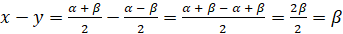 .
.
Поэтому 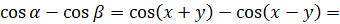 [
[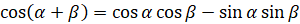 ,
, 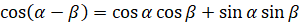 ]
] 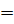
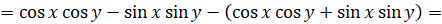
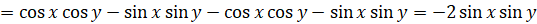 .
.
Вернёмся к замене и получим: 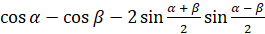 .
.
Читается формула следующим образом: разность косинусов двух углов равна взятому со знаком «минус» удвоенному произведению синуса полусуммы этих углов на синус их полуразности.
Таким образом, мы с вами познакомились с формулами суммы и разности синусов и формулами суммы и разности косинусов.
Давайте вычислим 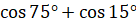 . Для этого воспользуемся формулой
. Для этого воспользуемся формулой 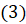 . Имеем:
. Имеем:
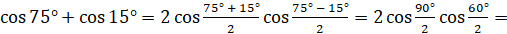
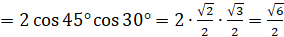 .
.
И преобразуем в произведение выражение:
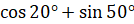 .
. 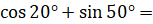 [запишем
[запишем 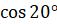 как
как 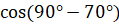 ]
] 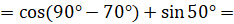 [
[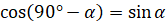 ]
] 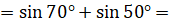
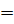 [воспользуемся формулой
[воспользуемся формулой 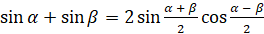 ]
] 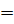
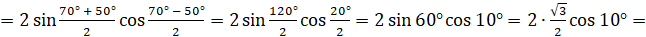
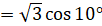 .
.
А сейчас рассмотрим следующие три формулы: 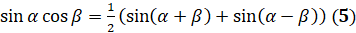 ,
, 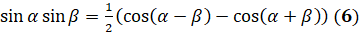 ,
, 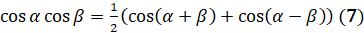 . Это формулы преобразования произведений в сумму или разность.
. Это формулы преобразования произведений в сумму или разность.
Давайте с вами докажем, например, формулу 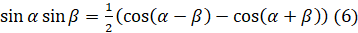 . Для этого преобразуем правую часть равенства к левой:
. Для этого преобразуем правую часть равенства к левой: 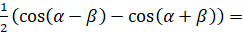 [к выражению в скобках применим формулу
[к выражению в скобках применим формулу 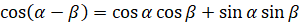 и формулу
и формулу 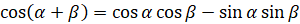 ]
]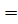
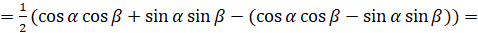
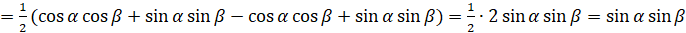 .
.
Итак, мы привели правую часть равенства к левой,
следовательно, доказали, что произведение синуса угла альфа и синуса угла бета
равно полуразности косинуса разности этих углов и косинуса их суммы. Формулы 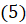 и
и 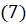 доказываются так же, как и формула
доказываются так же, как и формула 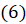 .
.
А теперь закрепим новые знания на практике.
Задание первое. Представьте в виде произведения следующие
выражения: а) 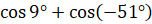 ; б)
; б) 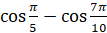 ; в)
; в) 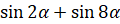 ; г)
; г) 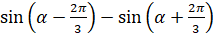 .
.
Решение.
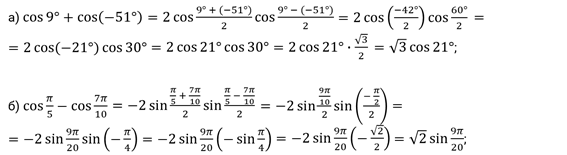
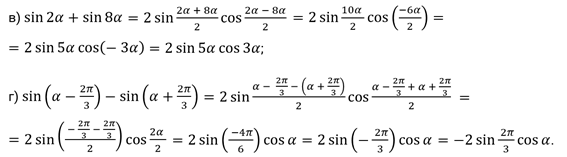
Второе задание. Представьте в виде суммы или разности выражения:
а) 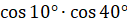 ; б)
; б) 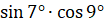 ; в)
; в)  .
.
Решение.
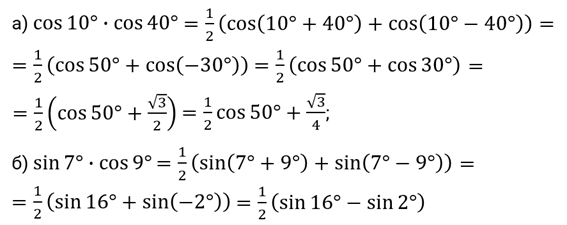
И выполним ещё одно задание, в котором
надо найти значения следующих выражений: а) 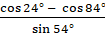 ; б)
; б) 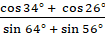 .
.
Решение.
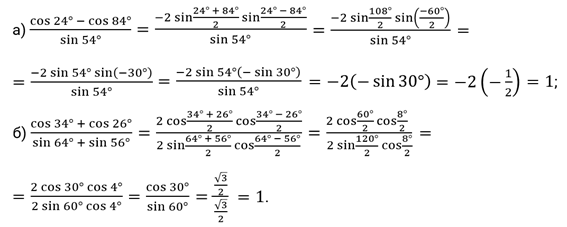

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 23532
23532

