Сила упругости, как и сила тяжести, является консервативной. Напомним, что консервативная сила — это такая сила, работа которой при движении тела по замкнутому контуру, равна нулю. В одном из уроков мы уже убедились, что работу силы упругости нельзя вычислить, пользуясь общей формулой для работы силы. Дело в том, что сила упругости изменяется с изменением растяжения или сжатия пружины. Поэтому нам необходимо будет воспользоваться графиком зависимости силы упругости от удлинения.
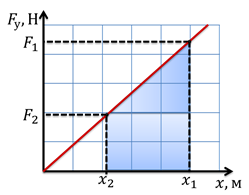
Поскольку сила упругости линейно зависит от удлинения, нам не составит труда найти площадь под графиком функции силы упругости. Эта площадь и будет являться работой. На графике зависимости силы упругости от удлинения обозначим два произвольных значения силы: F1 и F2. Этим значениям будут соответствовать значения удлинения х1 и х2. Как видно из графика, чтобы найти работу, нам нужно вычислить площадь трапеции. Площадь трапеции равна произведению полусуммы оснований и высоты. Очевидно, что основания — это F1 и F2, а высота равна х1 − х2. Тогда, используя формулу для силы упругости, мы можем вывести окончательное выражение для работы силы упругости:

Напомним, что изучая работу силы, мы пришли к выводу, что работа равна изменению кинетической энергии. В данном случае мы видим, что работа силы упругости равна изменению потенциальной энергии пружины. Но о потенциальной энергии мы поговорим немного позже.
Итак, мы выяснили, что работа силы упругости, так же, как и работа силы тяжести, не зависит от траектории движения.
Пример решения задачи.
Задача. Когда пружину, изначально находящуюся в расслабленном состоянии, растянули на 2 см, сила упругости составила 5 Н. Найдите работу силы упругости при растяжении этой пружины на 8 см.
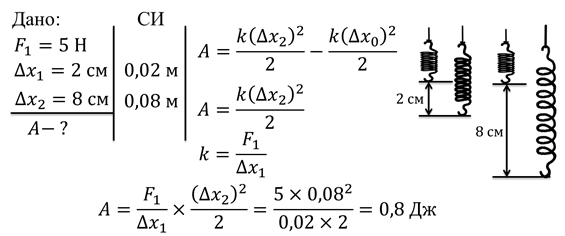

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 15618
15618

