Совсем недавно, мы изучили работу силы. Напомним, что работа силы равна произведению модуля силы, модуля перемещения и косинуса угла между направлениями силы и перемещения:

Рассмотрим теперь частный случай — работу силы тяжести при перемещении тела с высоты h1 на высоту h2.
Первый случай — это падение тела вертикально вниз.
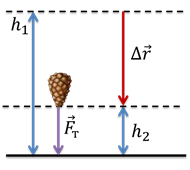
В этом случае, перемещение, конечно же, будет равно
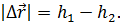
Сила тяжести, как мы знаем, равна
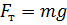 .
.
Поскольку сила тяжести направлена вертикально вниз, как и перемещение, косинус угла между направлениями этих векторов равен единице. Таким образом, мы получим, что работа силы тяжести равна:
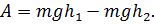
Второй случай — это когда тело, наоборот, подбрасывают вертикально вверх с высоты h1 на высоту h2.
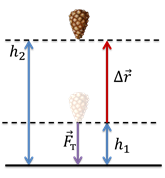
В этом случае, угол между направлением силы тяжести и направлением перемещения составит 180о. Это приводит нас к тому, что работа силы тяжести опять-таки равна:
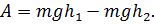
Наконец, рассмотрим случай, когда между направлением силы тяжести и перемещением существует произвольный угол α.
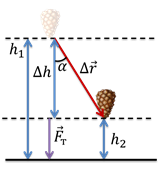
Обозначим модуль перемещения за s. В этом случае, работа силы тяжести равна:
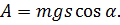
Но, исходя из определения косинуса:
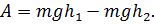
Таким образом, мы в третий раз получили одинаковый результат.
Более того, если даже мы рассмотрим криволинейную траекторию, то убедимся, что результат будет тем же.
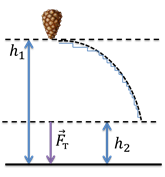
Любую кривую мы можем представить в виде ломаной линии, состоящей из очень маленьких горизонтальных и вертикальных отрезков. На горизонтальных отрезках работа силы тяжести будет равна нулю, поскольку в этом случае направление перемещения перпендикулярно направлению силы тяжести. На вертикальных участках работа будет равна: A = mg(s1 + … + sn). Очевидно, что эта сумма будет равна (h1 – h2):
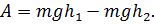
Таким образом, мы убедились, что работа силы тяжести не зависит от траектории движения тела. Имеет значение лишь то, насколько начальное положение тела отличается от конечного. Это плавно подводит нас к понятию потенциальной энергии, которое мы рассмотрим немного позже.
Из приведенных примеров вытекает еще один важный вывод: при движении тела по замкнутой траектории работа силы тяжести равна нулю. Для начала рассмотрим контур, имеющий форму прямоугольника. Как мы уже убедились, при движении тела в горизонтальном направлении, работа силы тяжести равна нулю. Вектор перемещения направлен перпендикулярно вектору силы тяжести. При перемещении же по противолежащим вертикальным сторонам контура, сила тяжести совершает работу, равную по абсолютной величине, но противоположную по знаку.
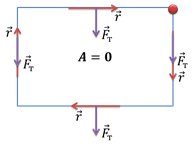
В одном случае вектор перемещения направлен так же, как вектор силы тяжести, а в другом — направлен в противоположную сторону. Это довольно логично, поскольку при движении тела вниз, сила тяжести ему «помогает», а при движении вверх — наоборот, мешает.
Мы можем сколь угодно усложнить эту траекторию, получив совершенно произвольный замкнутый контур.

Но опять же, разбив все кривые на ломаные линии с горизонтальными и вертикальными участками, мы убедимся, что суммарная работа будет равна нулю.
Силы, обладающие такими свойствами, называются консервативными. То есть, консервативная сила — это такая сила, работа которой в замкнутом контуре равна нулю.
Примеры решения задач.
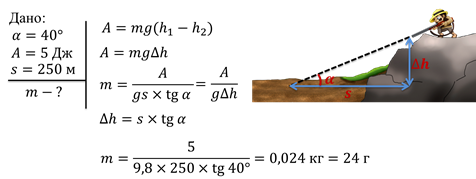
Задача 1. Охотник стреляет со скалы под углом 40° к горизонту. За время падения пули работа силы тяжести составила 5 Дж. Если пуля вошла в землю на расстоянии 250 м от скалы, то какова её масса?
Задача 2. Находясь на Нептуне, тело совершило перемещение так, как показано на рисунке. При этом перемещении работа силы тяжести составила 840 Дж. Если масса данного тела равна 5 кг, то каково ускорение свободного падения на Нептуне?


 Получите свидетельство
Получите свидетельство Вход
Вход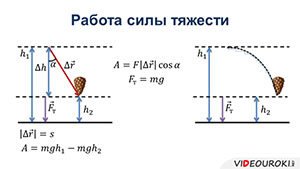



 0
0 21209
21209

