Вы знаете, что числа можно сравнивать. Давайте вспомним, какие числа вы уже умеете сравнивать:
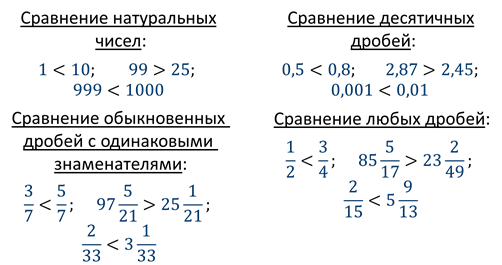
Следовательно, вы умеете сравнивать любые положительные числа друг с другом и с нулём. А как вы думаете, отрицательные числа можно сравнивать? Конечно! И отрицательные друг с другом, и отрицательные с положительными, и отрицательные с нулём. Сегодня на уроке мы об этом и поговорим.
Давайте начертим координатную прямую, отметим на ней начало отсчёта, выберем единичный отрезок и укажем направление.

Напомним, на горизонтальной координатной прямой положительные
числа изображаются правее нуля, а отрицательные – левее
нуля. Возьмём два числа, например, 1
и  .
Вы знаете, что
.
Вы знаете, что 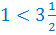 . Отметим на координатной прямой точки А(1) и В(
. Отметим на координатной прямой точки А(1) и В( ).
).

Понятно, что точка А на координатной прямой расположена левее точки В.
Напомним, правило: на горизонтальной координатной прямой точка с большей координатой лежит правее точки с меньшей координатой. Соответственно, на горизонтальной координатной прямой точка с меньшей координатой лежит левее точки с большей координатой.
А теперь давайте возьмём два отрицательных числа, например,
– 2 и –  .
Как сравнить такие числа? Отметим на координатной прямой точки С(– 2) и D(–
.
Как сравнить такие числа? Отметим на координатной прямой точки С(– 2) и D(–  ).
).

Запишем правило сравнения любых чисел:
Из двух чисел больше то, которое изображается на горизонтальной координатной прямой правее. И, соответственно, из двух чисел меньше то, которое изображается на горизонтальной координатной прямой левее.
Пример

Если рассматривать вертикальную координатную прямую, то в сформулированном правиле сравнения нужно заменить слово «правее» на «выше», а слово «левее» – на «ниже».
Сформулируем правило сравнения чисел на вертикальной координатной прямой.
Из двух чисел больше то, которое изображается на вертикальной координатной прямой выше. И, соответственно, из двух чисел меньше то, которое изображается на вертикальной координатной прямой ниже.
Хотелось бы сразу уточнить, что все положительные числа больше нуля, а все отрицательные – меньше нуля.

Любое отрицательное число меньше положительного.
Вообще очень удобно сравнивать числа при помощи понятия «модуль числа». Так как большее из двух положительных чисел на координатной прямой изображается правее, т.е. дальше от начала отсчёта, то это число имеет больший модуль.

Запомните, из двух положительных чисел больше то, чей модуль больше.
Так как большее из двух отрицательных чисел на координатной прямой изображается правее, т.е. ближе к началу отсчёта, то это число имеет меньший модуль.
Запомните, из двух отрицательных чисел больше то, чей модуль меньше.
Чтобы научиться легко сравнивать отрицательные числа, не пользуясь координатной прямой, давайте порассуждаем. Когда теплее – при – 25° или при – 5°?

Конечно, каждому понятно, что теплее при -5.
А сейчас забудем о температуре и зададим такой вопрос: какое из чисел -25 и -5 больше? Ясно, что

В чём можно убедиться, используя координатную прямую:

Задание
Расположите числа в порядке возрастания:
 .
.
Решение:

Задание
Расположите числа в порядке убывания:
 .
.
Решение:

Итоги
Из двух чисел больше то, которое изображается на горизонтальной координатной прямой правее. И, соответственно, из двух чисел меньше то, которое изображается на горизонтальной координатной прямой левее.
Все положительные числа больше нуля.
Все отрицательные – меньше нуля.
Любое отрицательное число меньше положительного.
Из двух положительных чисел больше то, чей модуль больше.
Из двух отрицательных чисел больше то, чей модуль меньше.

 Получите свидетельство
Получите свидетельство Вход
Вход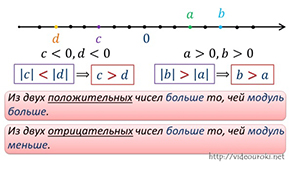



 0
0 6000
6000

