Получите свидетельство
Вход
Вопросы занятия:
· повторить, какие неравенства называются квадратичными;
· подробно рассмотреть такой способ решения квадратных неравенств как графический;
· вспомнить алгоритм решения таких неравенств.
Материал урока
Напомним, что квадратным неравенством называется неравенство вида:
Для решения такого рода неравенств как правило используют два основных метода решения: графический и аналитический метод или по-другому, метод интервалов. В любом случае, чтобы решить квадратное неравенство сначала надо решить соответствующее квадратное уравнение.
Сегодня мы с вами повторим графический метод решения квадратных неравенств.
Для того, чтобы применить этот способ, давайте вспомним, что графиком квадратичной функции является парабола.
Мы знаем, что если рассматривать не неравенство, а квадратное уравнение, то, в зависимости от знака дискриминанта у уравнения может не быть корней, быть один или два корня.
Графически решениями уравнения будут абсциссы точек пересечения параболы и оси Ох.
То есть можно составить таблицу, в которой графически будут изображены все случаи, пересечения параболы и оси Ох.
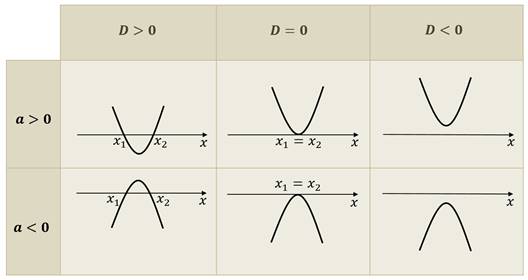
Найдя корни соответствующего квадратного уравнения, решить квадратное неравенство нетрудно.
Рассмотрим несколько примеров.
Пример.
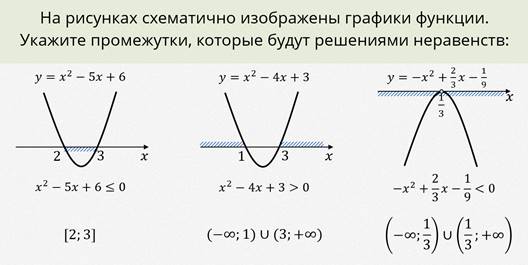
Для того, чтобы не заучивать таблицу, которую мы заполняли выше, давайте вспомним алгоритм решения квадратного неравенства.
1. Определить направление ветвей параболы.
2. Найти корни соответствующего квадратного уравнения или установить, что это уравнение не имеет корней.
3. Схематично изобразить график квадратичной функции, отмечая абсциссы точек пересечения графика с осью Ох.
4. По графику определить промежутки, которые будут решениями неравенства.
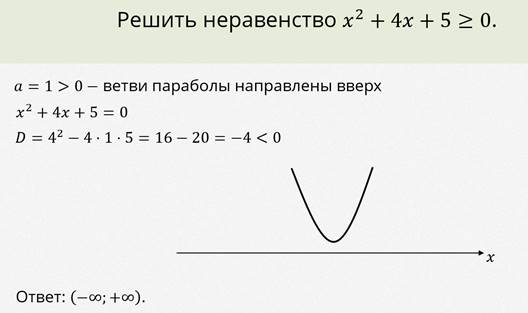
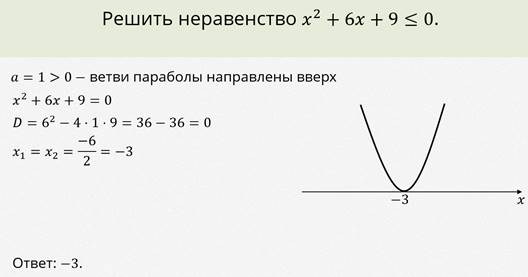
Рассмотрим пример.
Пример.
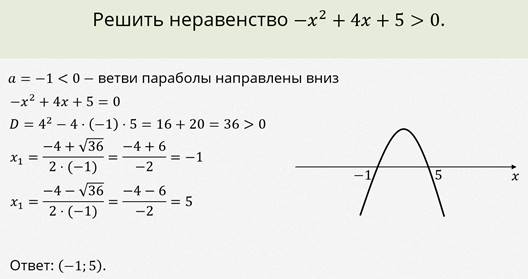
Рассмотрим ещё один пример.
Пример.
Рассмотрим ещё один пример.
Пример.
Итоги урока
Сегодня на уроке мы вспомнили какие неравенства называются квадратными, подробнее рассмотрели такой способ решения квадратных неравенств как графический. Вспомнили алгоритм решения таких неравенств.
0
12531
