Получите свидетельство
Вход
Вопросы занятия:
· повторить, какие выражения называются рациональными;
· повторить как решаются рациональные неравенства методом интервалов.
Материал урока
Определение.
Рациональные неравенства – это неравенства, обе части которых являются рациональными выражениями.
Определение.
Рациональное выражение – это алгебраическое выражение, составленное из чисел и переменной х с помощью операций сложения, вычитания, умножения деления и возведения в степень с натуральным показателем.
Один из видов рациональных неравенств, а именно, линейные неравенства, мы уже повторили. На сегодняшнем уроке мы поговорим о других рациональных неравенствах.
Рациональные неравенства бывают целыми, если в них нет операции деления на выражение, содержащее переменную.
Дробно-рациональными. Это неравенства, в которых есть операция деления на выражение, содержащее переменную.
Основным методом решения рациональных неравенств является метод интервалов.
Алгоритм решения неравенств методом интервалов прост:
1. Все члены неравенства перенести в левую часть, если неравенство дробно-рациональное, то привести левую часть к общему знаменателю.
2. Найти все значения переменной, при которых числитель и знаменатель обращаются в ноль.
3. Нанести найденные точки на числовую прямую, разбивая её при этом на интервалы, в каждом из которых рациональная функция сохраняет знак.
4. Определить знак функции на любом из интервалов.
5. Определить знаки на остальных интервалах: при переходе через точку знак меняется на противоположный, если точка является корнем нечётной степени кратности (то есть встречается нечётное количество раз среди корней числителя и знаменателя); при переходе через точку четной кратности знак сохраняется.
Здесь давайте вернёмся к теме многочлен и вспомним, что такое корни чётной и нечётной степени кратности.
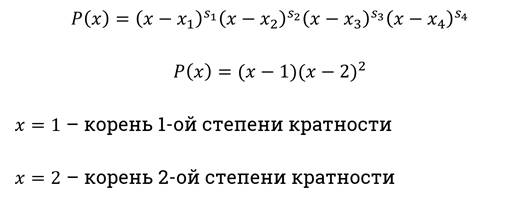
6. Множеством решений неравенства является объединение интервалов с соответствующим знаком функций. В случае нестрого неравенства к этому множеству добавляются корни числителя.
Рассмотрим использование этого алгоритма на примере.
Пример.
Пример.
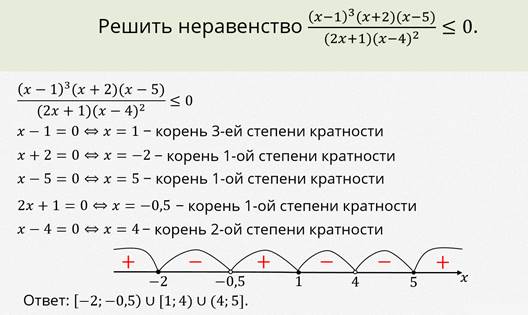
Пример.
Пример.
Итоги урока
Сегодня на уроке вы вспомнили какие неравенства называются рациональными. Вспомнили как решаются неравенства методом интервалов.
0
11004
