Линейные неравенства, содержащие переменную под знаком модуля

Вопросы занятия:

·  повторить основные методы решения линейных уравнений, содержащих переменную под знаком модуля.

Материал урока

Прежде чем мы приступим к решению неравенств, давайте вспомним, что такое модуль числа.

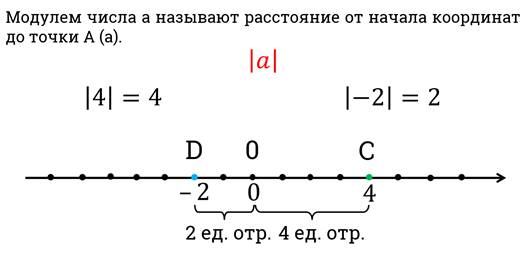
Поскольку модуль – это расстояние, то он не может принимать отрицательные значения.

Давайте вспомним свойства модуля действительного числа.

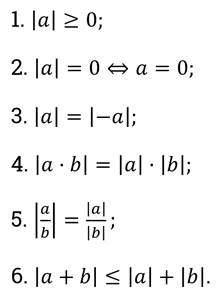
Начнём рассматривать простейшие неравенства вида:

И начнём с неравенств:

Неравенство графически можно изобразить так: расстояние от начала координат до точки икс меньше числа а. Мы знаем, что точки можно откладывать в обе стороны от начала координат. Точка, которая находится на расстоянии а от начала координат, отложенного влево, имеет координату минус а. Тогда те точки, расстояние до которых будет меньше а будут лежать левее начала координат, но правее точки с координатой минус а. То есть, точки, удовлетворяющие нашему неравенству, будут лежать в промежутке от минус а до а. Поскольку неравенство строгое, то концы промежутка не входят в решения.

Это же решение можно записать системой неравенств.

Пример.

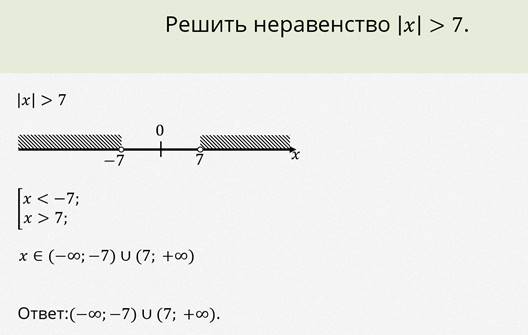
Теперь давайте рассмотрим неравенство:

Рассмотрим графическую интерпретацию этого неравенства.

Обратите внимание, что в решении у нас знак не системы неравенств, а совокупности. Знак совокупности обозначает, что должно выполнятся хотя бы одно из условий.

Например,

Знак же системы обозначает, что обязательно должны выполнятся оба условия.

Рассмотрим пример.

Пример.

Теперь давайте рассмотрим неравенства вида:

По свойству модуля, модуль не может быть отрицательным числом и, очевидно, что оно не может быть меньше отрицательного числа, то есть:

не имеет решений.

Теперь давайте рассмотрим неравенства вида:

Поскольку положительное число всегда больше любого из отрицательных чисел, значит, это неравенство будет превращаться в верное числовое неравенство при любом х. То есть решениями неравенств такого типа будет любое число.

Пример.

Теперь давайте рассмотрим неравенства вида:

Пример.

Рассмотрим пример.

Пример.

Рассмотрим несколько примеров.

Пример.

Итоги урока

Сегодня на уроке мы вспомнили что такое модуль числа, основные свойства модуля числа, рассмотрели простейшие неравенства с модулями.