«Не стыдно не знать, стыдно не учиться».
Задача
1.
В колебательном контуре напряжение на зажимах изменяется по закону 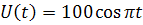 .
Найдите действующие значения силы тока и напряжения, если активное
сопротивление цепи равно 50 Ом.
.
Найдите действующие значения силы тока и напряжения, если активное
сопротивление цепи равно 50 Ом.
|
ДАНО:
|
РЕШЕНИЕ Запишем общее уравнение гармонических колебаний напряжения
Исходя из заданного по условию задачи уравнения
можно определить, что амплитудное напряжение равно
Из закона Ома для участка цепи
Тогда действующие значения напряжения и силы тока равны
|
|
|
Ответ: Uд = 70,7 В; Iд = 1,4 А.
Задача 2. В цепь параллельно включены катушка с индуктивностью 30 мГн и конденсатор с ёмкостью 50 мкФ. Действующее значение силы тока равно 10 А. Запишете уравнения, описывающие колебания тока и напряжения, а также найдите активное сопротивление цепи.
|
ДАНО:
|
СИ
|
РЕШЕНИЕ Уравнения гармонических колебаний для напряжения и силы тока имеют вид
Циклическая частота колебательного контура определяется по формуле
Действующие значения напряжения и силы тока рассчитываются по выражениям
Тогда амплитудное значение силы тока равно
Амплитудное значение напряжения можно рассчитать по формуле
С учетом рассчитанных значений уравнения гармонических колебаний примут вид
Активное сопротивление цепи определяется по формуле
|
|
|

Задача 3. Действующее значение напряжения в цепи с колебательным контуром составляет 50 В. Известно, что в некоторый момент времени t = 2 мс ток в цепи равен 2 А. Найдите индуктивность катушки, если ёмкость конденсатора равна 80 нФ,а активное сопротивление цепи равно 20 Ом. Сдвиг фаз равен нулю.
|
ДАНО:
|
СИ
|
РЕШЕНИЕ Запишем уравнения, описывающие колебания тока и напряжения в общем виде
Из закона Ома для участка цепи
Действующие значения напряжения и силы тока рассчитываются по формулам
Тогда амплитудные значения напряжения и силы тока равны
Циклическая частота колебательного контура определяется по формуле
С учётом рассчитанного значения амплитудной силы тока и формулы для расчёта циклической частоты колебательного контура уравнение гармонических колебаний силы тока примет вид
Т.к. по истечении 2 мс сила тока равна 2А, то
|
|
|
Ответ: 53 Гн.
Задача 4. Активное сопротивление колебательного контура равно 35 Ом, а частота колебаний равна 25 кГц. Найдите ёмкость конденсатора и индуктивность катушки.
|
ДАНО:
|
СИ
|
РЕШЕНИЕ Максимальная электрическая энергия колебательного контура
Максимальная магнитная энергия колебательного контура
Когда электрическая энергия максимальна, магнитная энергия равна нулю и наоборот, когда магнитная энергия максимальна, электрическая энергия равна нулю. Поэтому, оба выражения для максимальной энергии соответствуют полной энергии контура. В общем случае в контуре с активным сопротивлением происходят потери энергии. Однако, в течение одного колебания эти потери ничтожно малы, поэтому можно приравнять максимальную электрическую и максимальную магнитную энергию.
Частота колебательного контура определяется по формуле
Преобразуем данное выражение
Активное сопротивление определяется по формуле
Из равенства максимальной электрической энергии и максимальной магнитной энергии получаем
Получаем систему состоящую из двух уравнений
Из первого уравнения получаем
Из второго уравнения
|
|
|
Ответ: L = 2,2×10–4 Гн; C = 1,7×10–7 Ф.

 Получите свидетельство
Получите свидетельство Вход
Вход






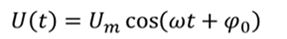
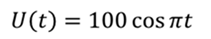





























































 0
0 13175
13175

