«Самые совершенные радиоприёмники
и самая сложная аппаратура для сигнализации,
автоматики и телеуправления будут иметь
ничтожные габариты и во много раз дешевле»
Абрам Иоффе
Данная тема посвящена решению задач на свободные колебания в колебательном контуре.
Задача
1.
Заряд на обкладках конденсатора с ёмкостью 5 нФ изменяется по закону  .
Найдите амплитуду колебаний заряда конденсатора и индуктивность катушки,
предполагая, что катушка и конденсатор составляют идеальный колебательный
контур.
.
Найдите амплитуду колебаний заряда конденсатора и индуктивность катушки,
предполагая, что катушка и конденсатор составляют идеальный колебательный
контур.
|
ДАНО:
|
РЕШЕНИЕ Уравнение гармонических колебаний заряда имеет вид
Исходя из заданного уравнения в условии задачи амплитуда заряда и циклическая частота колебаний равны
Циклическая частота колебательного контура определяется по формуле
Выразим из данной формулы индуктивность катушки
|
|
|
Ответ: qm = 10–5 Кл, L = 0,2 Гн.
Задача 2. Амплитуда напряжения в контуре равна 200 В. Известно, что в момент времени t = 25 мкс напряжение в первый раз становится равно 120 В. Найдите частоту колебаний в контуре.
|
ДАНО:
|
СИ
|
РЕШЕНИЕ Запишем общее уравнение, описывающее колебания напряжения в контуре
С учётом исходных данных можно записать
Циклическая частота определяется по формуле
Тогда
|
|
|
Ответ: 5903 Гц.
Задача 3. Колебательный контур состоит из конденсатора с ёмкостью 0,1 мкФ и катушки с индуктивностью 20 мГн. Известно, что амплитуда напряжения в контуре равна 100 В. Постройте график зависимости силы тока в цепи от времени.
|
ДАНО:
|
СИ
|
РЕШЕНИЕ Запишем уравнения, описывающие изменение силы тока и напряжения в контуре
Из первого уравнения ясно, что амплитудное напряжение равно отношению максимального заряда к ёмкости конденсатора
Из второго уравнения ясно, что амплитудный ток равен произведению максимального заряда и циклической частоты
Циклическая частота колебательного контура определяется по формуле
Амплитудный ток равен
Циклическая частота равна
Исходя из вычисленных значений уравнение, описывающие изменение силы тока в контуре примет вид
Построим график зависимости силы тока в цепи от времени. Для этого рассчитаем период колебаний
|
|
|
Задача 4. В колебательном контуре за 1 мс 200 раз достигается максимальное значение электрической и магнитной энергии. Если максимальное значение силы тока равно 300 мА, найдите электрическую энергию контура в момент времени t = 0,6 T. Ёмкость конденсатора равна 2 мкФ.
|
ДАНО:
|
СИ
|
РЕШЕНИЕ Максимальная электрическая энергия колебательного контура определяется по формуле
Максимальная магнитная энергия колебательного контура равна
Максимальное значение электрической или магнитной энергии в контуре достигается дважды за 1 период колебаний.
Период колебаний определяется по формуле
Циклическая частота рассчитывается по выражению
Циклическую частоту колебательного контура можно также определить по формуле
Из последней формулы следует
Амплитудное напряжение
Тогда получаем, что
С учётом того, что
Уравнение гармонических колебаний
примет вид
Т.к. по условию
то получаем
Тогда электрическая энергия колебательного контура равна
|
|
|
Ответ: 57 нДж.
Задача 5. В колебательном контуре происходят незатухающие электромагнитные колебания с частотой 105 Гц. При добавлении в контур ещё одного конденсатора с ёмкостью 10–10 Ф, частота увеличилась втрое. Найдите индуктивность катушки и ёмкость первого конденсатора.
|
ДАНО:
|
РЕШЕНИЕ
Запишем формулу для расчёта частоты колебательного контура
Из формулы видно, что ёмкость конденсатора находится в знаменателе, а частота, по условию задачи, увеличилась. Следовательно, при включении второго конденсатора, общая электроёмкость участка с этими двумя конденсаторами уменьшилась. Запишем правила последовательного и параллельного соединения конденсаторов. При последовательном соединении
При параллельном соединении
Исходя из этих правил, при параллельном соединении электроёмкости конденсаторов суммируются, а, значит, общая электроёмкость участка увеличивается. Поэтому, второй конденсатор был подключен последовательно.
Применим правила последовательного соединения, чтобы найти общую электроёмкость конденсаторов
Запишем выражения для начальной и конечной частоты колебаний контура
Также по условию задачи известно
Рассмотрим отношение начальной и конечной частоты колебаний контура
Преобразуем данное отношение
Теперь определим индуктивность катушки
|
|
|
Ответ: C1 = 8×10–10 Ф; L = 3,2 мГн.

 Получите свидетельство
Получите свидетельство Вход
Вход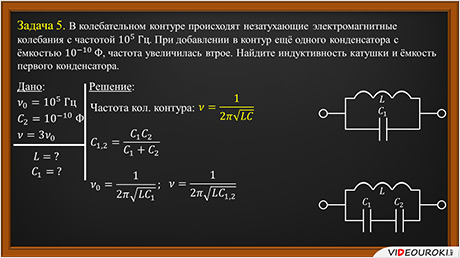





















































































 0
0 7258
7258

