Основные формулы и методические рекомендации по решению задач на электромагнитные колебания

«Все, что казалось трудным нам сначала,

к концу обычно трудным не бывало».

Данная тема посвящена рассмотрению основных формул и методических рекомендаций по решению задач на электромагнитные колебания.

В данном разделе будут рассматриваться случаи, в которых колеблющиеся величины совершают гармонические колебания. Итак, гармонические колебания – это повторяющийся во времени процесс отклонения системы от положения равновесия, при котором не происходят потери энергии, и который подчиняется синусоидальному закону. Соответственно, зависимости от времени таких величин, как напряжение, заряд, сила тока и так далее будут представлять собой синусоиды.

Колебательный контур – это осциллятор, представляющий собой электрическую цепь, содержащую соединённые катушку индуктивности и конденсатор. В такой цепи могут возбуждаться колебания тока и напряжения.

Следует отметить, что контур, в котором не происходят потери энергии, называется идеальным колебательным контуром или контуром Томсона. В соответствии с определением идеального контура, Томсон вывел формулу, по которой вычисляется период колебаний в таком контуре. В реальных контурах, конечно, существует активное сопротивление, а, значит, происходят потери энергии. Поэтому, без дополнительного поступления энергии, колебания являются затухающими.

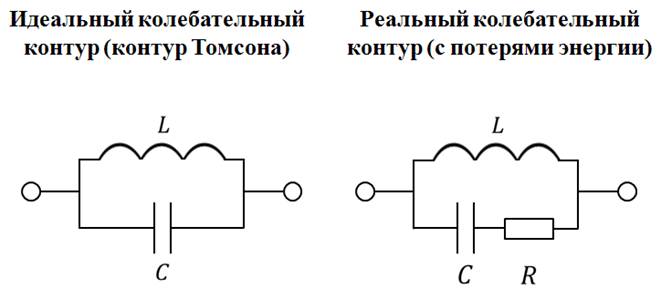
Рассмотрим параметры и характеристики этих колебаний.

В электромагнитных колебаниях амплитудой колебаний называется максимальное значение колеблющейся величины. Для примера рассмотрим график, описывающий гармонические колебания. Максимальные значения колеблющейся величины соответствуют пикам синусоиды. Что касается фазы, то это величина, определяющая смещение в любой момент времени (то есть, состояние системы). Если мы обозначим на графике вторую синусоиду, то фазой будет расстояние между двумя ближайшими пиками этих синусоид (хотя, чаще фаза измеряется в радианах).

Периодом колебаний называется время одного полного колебания (то есть, за это время повторяются какие-либо показатели системы). Для примера рассмотрим график, описывающий гармонические колебания. Расстояние между двумя ближайшими пиками синусоиды – это и будет промежуток времени, по прошествии которого повторились показатели системы (в данном случае, это отклонение от положения равновесия). Частота колебаний – это величина, обратная периоду, то есть, число колебаний в единицу времени.

Циклическая частота – это физическая величина, численно равная количеству колебаний за 2p секунд. То есть, это тоже самое, что и частота, только в качестве единиц времени взято 2p (таким образом, циклическая частота измеряется в радианах в секунду).

Собственная частота – это частота колебаний системы при отсутствии сил сопротивления в среде (в случае электромагнитных колебаний это подразумевает отсутствие активного сопротивления).

С электромагнитными колебаниями, конечно, связано понятие переменного тока. Переменный ток с успехом используется в трансформаторах. Трансформатор – это устройство, служащее для преобразования силы инапряжения переменного тока принеизменной частоте. Простейший трансформатор состоит их двух катушек индуктивности, соединённых сердечником. Работа трансформаторов основана на явлении электромагнитной индукции. За счёт неравного количества витков в катушках можно повышать или понижать напряжение, подаваемое на первичную обмотку.

Сведём в таблицу основные формулы электромагнитных колебаний.

Методические рекомендации по решению задач на применение общих уравнений гармонических колебаний

1. Записать общее уравнение гармонических колебаний.

2. Если в задаче есть заданное уравнение колебаний, сопоставить его с общим уравнением и определить параметры электромагнитных колебаний.

3. Если в задаче даны характеристики электромагнитных колебаний, составить соответствующее уравнение, опираясь на них.

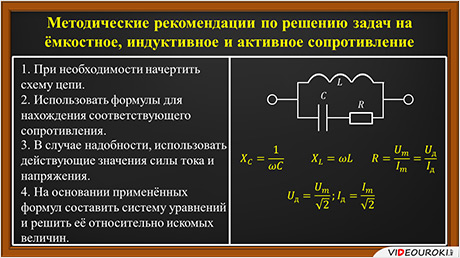
Методические рекомендации по решению задач на ёмкостное, индуктивное и активное сопротивление.

1. При необходимости начертить схему цепи.

2. Использовать формулы для нахождения соответствующего сопротивления.

3. В случае надобности, использовать действующие значения силы тока и напряжения.

4. На основании применённых формул составить систему уравнений и решить её относительно искомых величин.

Методические рекомендации по решению задач на закон Ома для цепей переменного тока.

1. Начертить схему цепи.

2. Использовать формулу для нахождения полного сопротивления.

3. Применить закон Ома для цепей переменного тока.

4. В случае надобности, найти разность фаз.

5. На основании применённых формул составить систему уравнений и решить её относительно искомых величин.

Методические рекомендации по решению задач на трансформаторы.

1. Рассмотреть напряжения или токи в обмотках, мощность нагрузки, рабочий или холостой ход трансформатора.

2. Применить формулу для коэффициента трансформации.

3. В случае надобности воспользоваться законом Ома для замкнутой цепи.

4. При необходимости, применить формулу для КПД трансформатора.

5. На основании применённых формул составить систему уравнений и решить её относительно искомых величин.