«Мир, в котором мы живём,
удивительно склонен к колебаниям….
Колеблются даже атомы,
из которых мы состоим».
Данная тема посвящена решению задач на пружинный маятник.
Задача 1. На пружину с жёсткостью 50 Н/м подвешивают груз массой 3 кг. За какое время груз совершит 30 полных колебаний?
|
ДАНО:
|
РЕШЕНИЕ Период колебаний пружинного маятника может быть определён по формуле
Период колебаний, в общем случае также рассчитывается по формуле
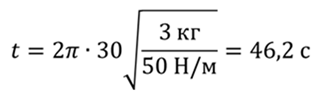
Приравняем эти формулы и выразим искомое время
|
|
|
Ответ: 46,2 с.
Задача 2. К пружине подвешен груз массой 100 г. После того, как массу груза увеличили, период колебаний увеличился в 2,5 раза. Найдите массу, на которую увеличили массу груза.
|
ДАНО:
|
СИ
|
РЕШЕНИЕ Период колебаний пруженного маятника определяется по формуле
Применим эту формулу для начального и конечного периодов
Т.к. по условию задачи
То получаем
Преобразуем данное выражение
|
|
|
Ответ: 525 г.
Задача 3. Шарик массой 400 г подвешен на пружине. Собственная частота колебаний шарика равна 15 рад/с, а начальная амплитуда колебаний равна 40 см. Известно, что система теряет энергию со скоростью 2 Дж/с. Через какое время после начала затухания колебаний шарик остановится?
|
ДАНО:
|
СИ
|
РЕШЕНИЕ Энергия пружинного маятника рассчитывается по формуле
Собственная частота пружинного маятника определяется по формуле
Выразим из этой формулы коэффициент жёсткости и подставим его в первую формулу
Составим уравнение, учитывая то, что шарик остановится в тот момент, когда система исчерпает свою энергию (то есть, начальная энергия будет уменьшаться с указанной в задаче скоростью, в течение определённого промежутка времени)
|
|
|
Ответ: 3,6 с.
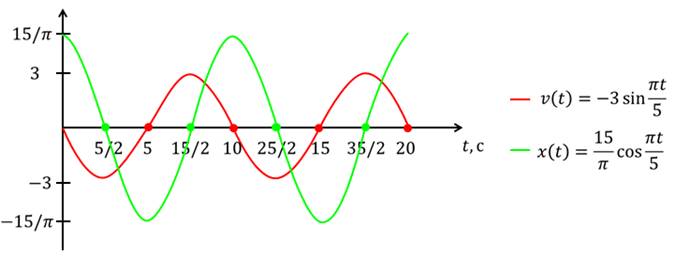
Задача 4. Пружинный маятник совершает колебания по закону косинуса. Известно, что максимальная скорость, достигаемая системой при колебаниях равна 3 м/с, а период колебаний составляет 10 с. Постройте графики зависимости координаты и скорости от времени. Сдвиг фаз равен нулю.
|
ДАНО:
|
РЕШЕНИЕ Запишем уравнение гармонических колебаний
Циклическую частоту пружинного маятника можно рассчитать по формуле
С другой стороны циклическая частота определяется как
Запишем закон сохранения энергии для пружинного маятника
При колебаниях потенциальная энергия переходит в кинетическую и наоборот, поэтому, полную энергию можно приравнять к максимальной кинетической или максимальной потенциальной энергии.
Приравняем эти две формулы и выразим амплитуду
Тогда с учетом значений амплитуды и циклической частоты уравнение гармонических колебаний примет вид
Скорость гармонических колебаний описывается уравнением
Тогда получаем
По полученным зависимостям построим требуемые в условии задачи графики
|
|
|
Задача 5. Шарик, прикреплённый к пружине, совершает колебания в горизонтальной плоскости с периодом 5 с. Если эту пружину заменить на другую, то период колебаний станет равен 8 с. Найдите период колебаний, системы, состоящей из этих двух пружин и шарика (пружины соединяются последовательно).
|
ДАНО:
|
РЕШЕНИЕ Период колебаний пружинного маятника определяется по формуле
Применим эту формулу к первому и второму значению периода и выразим из этих формул коэффициенты жёсткости пружин
При некотором сжатии (или растяжении) в каждой из пружин возникнут силы упругости. Пусть в пружине, конец которой зафиксирован, возникает сила упругости F1 (которая будет действовать на вторую пружину). В свою очередь, во второй пружине тоже возникнет сила упругости, которая будет действовать на первую пружину (обозначим её за F2). Запишем закон Гука
Применим его для сил F1 и F2
Очевидно, что смещение шарика будет определяться как
Тогда
Тогда период колебаний пружинного маятника
|
|
|
Ответ: 9,43 с.

 Получите свидетельство
Получите свидетельство Вход
Вход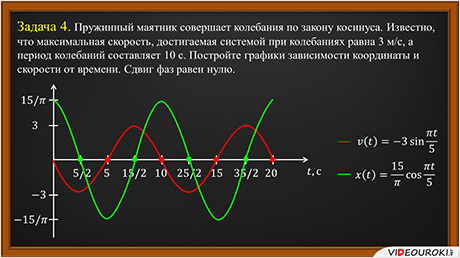



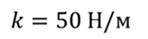
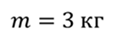
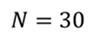
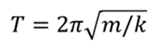
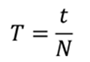
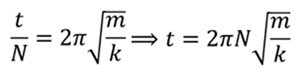
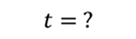
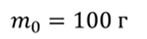
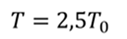
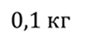
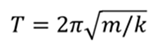
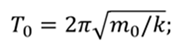
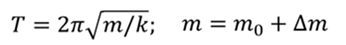
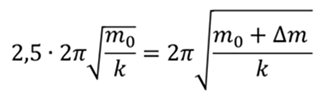
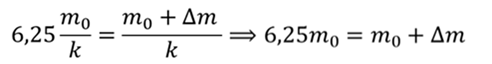
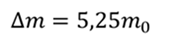
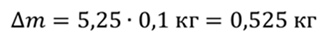
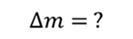
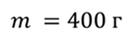
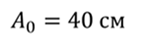
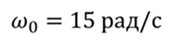
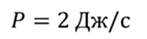
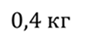
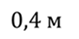
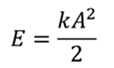
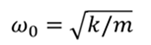
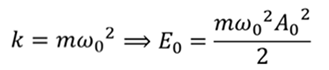
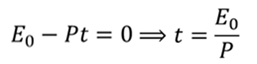
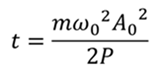
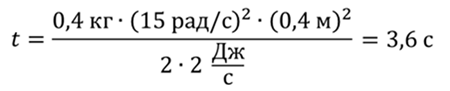
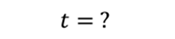
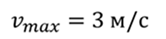
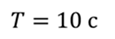
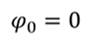
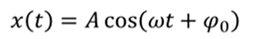
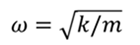
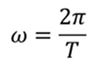
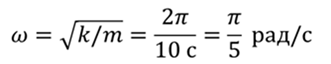
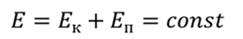
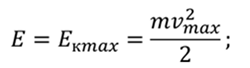
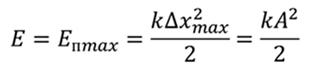
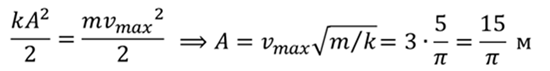
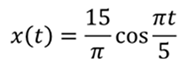
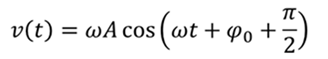
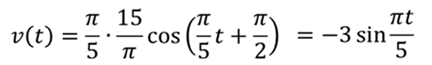
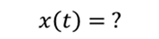
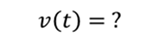
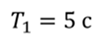
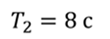
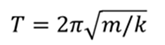
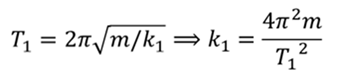
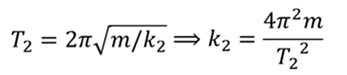
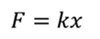
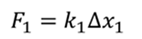
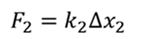



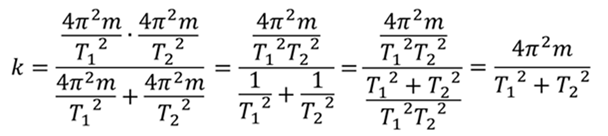



 0
0 5390
5390