«Мир, в котором мы живём,
удивительно склонен к колебаниям….
Колеблются даже атомы,
из которых мы состоим».
Данная тема посвящена решению задач на математический маятник.
Задача 1. Математический маятник совершил 30 колебаний за минуту. Найдите период и частоту колебаний, а также длину маятника.
|
ДАНО:
|
СИ
|
РЕШЕНИЕ Период колебаний можно определить по формуле
Частота колебаний рассчитывается по формуле
Период колебаний математического маятника рассчитывается также по формуле
Преобразуем эту формулу и выразим из неё длину маятника
|
|
|
Ответ: период – 2 с, частота – 0,5 Гц, длина маятника – 99 см.
Задача 2. При уменьшении длины математического маятника на 2 см, период его колебаний уменьшается в 1,5 раза. Найдите первоначальную длину маятника.
|
ДАНО:
|
СИ
|
РЕШЕНИЕ Период колебаний математического маятника определяется по формуле
В соответствии с этим, составим выражения для начального и конечного периода колебаний
Т.к. период колебаний уменьшился в 1,5 раза, то получаем
Преобразуем полученную формулу
|
|
|
Ответ: 3,6 см.
Задача 3. Математический маятник, проходя нижнюю точку имеет скорость 1 м/с, а его длина равна 20 см. Определите вертикальное отклонение маятника от положения равновесия в момент времени t = 5 с, если в начальный момент времени маятник находится на максимальной высоте.
|
ДАНО:
|
СИ
|
РЕШЕНИЕ Поскольку в начальный момент времени отклонение максимально, мы можем заключить, что маятник колеблется по закону косинуса. Запишем уравнение гармонических колебаний в общем виде
Исходя из начального условия, сдвиг фаз равен нулю. Очевидно, что максимальное значение y – это и есть амплитуда колебаний.
Запишем закон сохранения энергии, который выполняется для математического маятника
Тогда
Циклическая частота математического маятника рассчитывается по формуле
Т.к амплитуда и циклическая частота соответственно равны
То уравнение гармонических колебаний представленного математического маятника примет вид
А по прошествии 5 с
|
|
|
Ответ: 4,5 см.
Задача 4. Шарик массой 200 г, подвешенный на нити совершает колебания. Шарику сообщили заряд 300 мкКл и поместили всю систему в электростатическое поле, линии напряжённости которого направлены вертикально вниз. После этого циклическая частота колебаний увеличилась вдвое. Найдите напряжённость поля.
|
ДАНО:
|
СИ
|
РЕШЕНИЕ
Циклическая частота математического маятника определяется по формуле
Сила тяжести
Электростатическая сила равна произведению заряда и напряжённости электрического поля
В электростатике заряд – это величина, аналогичная массе в механике. Ускорение свободного падения – это силовая характеристика гравитационного поля, а напряжённость – это силовая характеристика электрического поля. Поэтому, необходимо найти, так называемое, эффективное ускорение свободного падения, в соответствии с тем, что на маятник действует ещё и электростатическая сила
Запишем теперь выражение для начальной циклической частоты (то есть, до сообщения шарику заряда)
Для конечной циклической частоты
Т.к. по условию задачи
Преобразуем данную формулу и выразим из неё Напряженность поля
|
|
|
Ответ: 1960 Н/Кл.
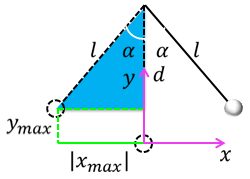
Задача 5. Материальная точка на нерастяжимой нити длиной 0,3 м совершает колебания, так что максимальный угол отклонения нити от вертикали составляет 30º. Найдите положение материальной точки в момент времени t = 5 с в системе отсчёта, связанной с положением равновесия. В начальный момент времени точка находится в положении равновесия.
|
ДАНО:
|
РЕШЕНИЕ
Запишем уравнение гармонических колебаний для каждой оси с учетом того, что сдвиг фаз равен нулю
Очевидно, что амплитуда равны максимальным отклонениям
Циклическая частота математического маятника определяется по формуле
Тогда с учётом того, что
Уравнения гармонических колебаний для каждой оси принимают вид
Тогда координаты точки через 5 с равны
|
|
|
Ответ: (–4,8 см; 1,3 см).

 Получите свидетельство
Получите свидетельство Вход
Вход






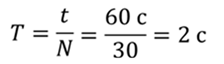



































































 0
0 13429
13429

