«Чем полнее вы сумеете сконцентрироваться
на единственной задаче, тем дальше
продвинетесь по «кривой производительности»:
время работы будет сокращаться, качество — расти»
Брайан Трейси
В данной теме будут разобраны примеры решений задач на равномерное прямолинейное движение.
Задача 1. Движение тела задано уравнением x = A + Bt, где А = 7,5 км, а B = –125 дм/с. Какой путь пройдет тело за 4 секунды своего движения?
|
ДАНО:
|
СИ
|
РЕШЕНИЕ: Рассмотрим заданное по условию задачи уравнение
Сравним полученное уравнение движения тела с кинематическим уравнением равномерного движения
Из сравнения уравнений следует
Теперь определим координату тела через четыре секунды, после начала отсчета времени
Для того чтобы определить путь, пройденный телом, необходимо найти разность, между конечной и начальной координатой тела. При этом помним, что путь — величина всегда положительная, поэтому разность координат находим по модулю
2 способ: При равномерном прямолинейном движении тела направление его скорости не меняется, тогда путь, пройденный телом, можно определить, как произведение модуля проекции скорости и времени движения
|
|
|
Ответ: 50 м.
Задача 2. Движение двух велосипедистов заданы уравнениями x1 = 5t (м) и x2 = 60 – 10t (м). Определите время и координату встречи велосипедистов.
|
ДАНО:
|
РЕШЕНИЕ: Сравним уравнения, которыми описываются их движения с кинематическим уравнением равномерного движения
Из данных уравнений следует, что для первого велосипедиста
Для второго велосипедиста
Значит, оба велосипедиста участвуют в равномерном прямолинейном движении. Свяжем систему отсчета с Землей, ось «О икс» направим в сторону движения первого велосипедиста, а за начало отсчета координаты выберем точку «О», то есть положение первого велосипедиста в начальный момент времени.
Два тела встречаются тогда, когда их координаты в этот момент времени совпадают, то есть равны.
Время встречи равно
Координата встречи равна
Графический метод: Ранее было выяснено, что велосипедисты движутся равномерно и прямолинейно. Поэтому графиком движения каждого из них будет являться прямая линия. Из курса математики вы должны знать, что для построения прямой линии достаточно найти какие-либо две ее точки.
На графике хорошо видно, что прямые пересеклись в одной точке — в точке места встречи. Для того чтобы определить ее координаты, опустим из этой точки два перпендикуляра — один на ось времени, а другой на ось координат |
Ответ: t0 = 4 с; х0 = 20 м.
Задача 3. Самолет взлетает с аэродрома под углом 30о к горизонту со скоростью 216 км/ч. Какой высоты самолет достигнет через 12 с и на какое расстояние в горизонтальном направлении он удалится от места взлета? Считать, что самолет в горизонтальном и вертикальном направлении движется с постоянной по модулю скоростью.
|
ДАНО:
|
СИ
|
РЕШЕНИЕ:
Запишем кинематические уравнения движения для каждого из случаев
В момент времени t:
Тогда
|
|
|
Ответ: l = 612 м; h = 360 м.
Задача 4. На первой половине маршрута автобус двигался со скоростью в 4 раза большей чем скорость, с которой он двигался на второй половине маршрута. Средняя скорость автобуса на всем пути составила 32 км/ч. Определите скорость автобуса на каждом участке пути.
|
ДАНО:
|
РЕШЕНИЕ: У многих может возникнуть желание произвести следующие действия, для решения данной задачи:
Но это не верно!!! Еще раз повторим, что не следует путать понятие «среднее значение величины» со среднеарифметическим значением. Согласно определению, средняя скорость движения определяется как отношение ВСЕГО ПРОЙДЕННОГО ПУТИ КО ВСЕМУ ЗАТРАЧЕННОМУ ВРЕМЕНИ (включая остановки и задержки).
|
|
|
Ответ: υ1 = 80 км/ч; υ2 = 20 км/ч.

 Получите свидетельство
Получите свидетельство Вход
Вход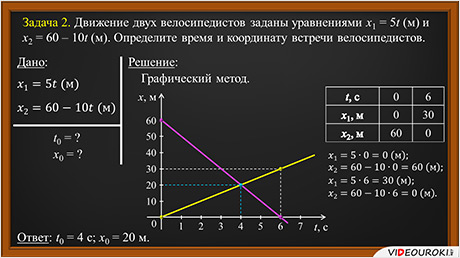
































































 0
0 8267
8267

