Пусть каждому натуральному  по
определённому правилу ставится в соответствие число
по
определённому правилу ставится в соответствие число 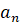 .
.
Получается упорядоченный ряд чисел 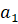 ,
, 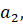 …
…
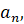 …, который
называют числовой последовательностью.
…, который
называют числовой последовательностью.
Числа 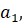 ,
, 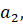 … называются
членами последовательности;
… называются
членами последовательности;
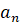 называется
называется  -й или общим
членом последовательности.
-й или общим
членом последовательности.
Сама последовательность обозначается 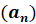 .
.
Последовательность считается заданной, если известно правило, по
которому каждому натуральному числу  ставится в
соответствие число
ставится в
соответствие число 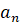 .
.
Такое соответствие устанавливается либо формулой общего члена последовательности, либо рекуррентной формулой общего члена последовательности, позволяющей вычислить члены последовательности по известным предыдущим.
Напомним, что арифметической прогрессией называется числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же для данной последовательности числом.
Если дана арифметическая последовательность 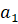 ,
, 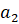 ,
, 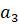 , …, то
, …, то 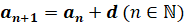 , где
, где 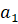 и
и 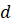 – любые заданные числа.
– любые заданные числа.
Число 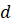 называется разностью
арифметической прогрессии.
называется разностью
арифметической прогрессии.
Для  -го члена
арифметической прогрессии справедлива формула:
-го члена
арифметической прогрессии справедлива формула:
 .
.
Необходимое и достаточное условия существования арифметической прогрессии.
Для того чтобы последовательность 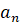 была
арифметической прогрессией, необходимо и достаточно, чтобы для любого
была
арифметической прогрессией, необходимо и достаточно, чтобы для любого  выполнялось
равенство:
выполнялось
равенство:
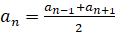 .
.
Давайте вспомним свойства арифметической прогрессии.
1. Для  первых
членов арифметической прогрессии
первых
членов арифметической прогрессии 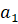 ,
, 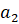 , …,
, …, 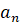 справедливо:
справедливо:

Это свойство называется основным свойством арифметической прогрессии.
2. Сумма  первых
членов арифметической прогрессии равна
первых
членов арифметической прогрессии равна
 .
.
Напомним, что геометрической прогрессией называется числовая последовательность, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число.
Если дана геометрическая последовательность  ,
,  ,
,  , …, то
, …, то 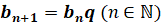 , где
, где  и
и  – любые
отличные от нуля числа.
– любые
отличные от нуля числа.
Число  называется знаменателем
геометрической прогрессии.
называется знаменателем
геометрической прогрессии.
Для  -го
геометрической прогрессии справедлива формула:
-го
геометрической прогрессии справедлива формула:
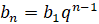 .
.
Необходимое и достаточное условия существования геометрической прогрессии.
Для того чтобы последовательность  была
геометрической прогрессией, необходимо и достаточно, чтобы для любого
была
геометрической прогрессией, необходимо и достаточно, чтобы для любого  выполнялось
равенство:
выполнялось
равенство:
 .
.
Давайте вспомним свойства геометрической прогрессии.
1. Если все члены геометрической прогрессии положительные, то каждый член геометрической прогрессии, начиная со второго, равен среднему геометрическому его соседних членов:
 .
.
2. Для  первых
членов геометрической прогрессии
первых
членов геометрической прогрессии  ,
,  ,
,  , …,
, …,  справедливо:
справедливо:
 .
.
Это свойство называется основным свойством геометрической прогрессии.
3. Сумма  первых
членов
первых
членов  геометрической прогрессии равна
геометрической прогрессии равна
 , если
, если  ;
;
 , если
, если  .
.
4. Если прогрессия – бесконечно убывающая, то есть 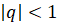 , то сумма
всех её членов равна
, то сумма
всех её членов равна
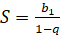 .
.
Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.
Задание первое. Сумма 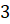 -го и
-го и 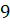 -го членов
геометрической прогрессии равна
-го членов
геометрической прогрессии равна  . Найдите
сумму её первых
. Найдите
сумму её первых 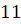 членов.
членов.
Решение.

Задание второе. Найдите числа, одновременно
входящие в 100 первых членов арифметической прогрессии  ,
, 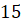 ,
, 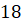 , … и
геометрической прогрессии 1
, … и
геометрической прогрессии 1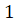 ,
, 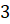 ,
,  , … .
, … .
Решение.
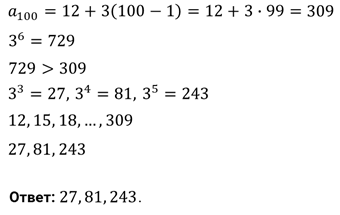
Задание третье. Сумма  -го и
-го и  -го членов
геометрической прогрессии равна 99, знаменатель равен 2. Найдите
-го членов
геометрической прогрессии равна 99, знаменатель равен 2. Найдите  -й член прогрессии.
-й член прогрессии.
Решение.
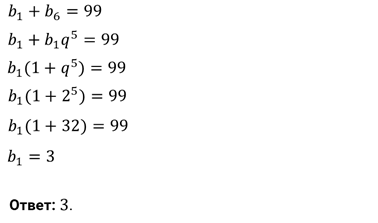
Задание четвёртое. Сумма первых трёх членов геометрической прогрессии равна 13, а сумма их квадратов – 91. Найдите эти числа.
Решение.

Задание пятое. Найдите сумму всех положительных чётных двузначных чисел, делящихся на 3 нацело.
Решение.

Задание шестое. Найдите сумму чисел 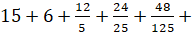 …. .
…. .
Решение.
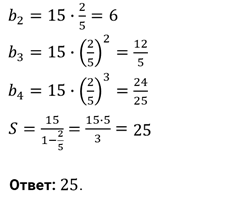
Задание седьмое. Три брата, возрасты которых образуют геометрическую прогрессию, делят между собой сумму денег пропорционально своему возрасту. Если бы они это проделали через 3 года, когда самый младший брат окажется вдвое моложе самого старшего, то младший бы получил на 105, а средний на 15 рублей больше, чем сейчас. Сколько лет каждому из братьев?
Решение.

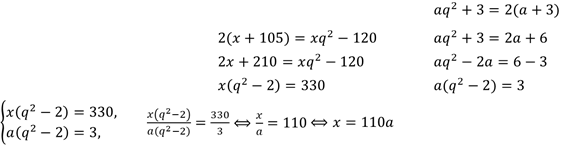

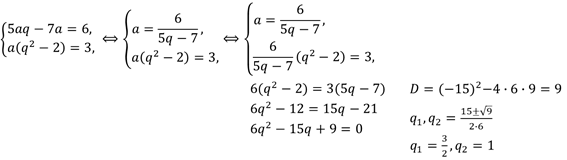


 Получите свидетельство
Получите свидетельство Вход
Вход




 2523
2523

