Напомним, что два числа, равные по модулю, но противоположные по знаку, называются противоположными.
Натуральные числа, противоположные им числа и число 0 составляют
вместе множество целых чисел. Множество целых чисел обозначается 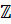 .
.
Число вида  , где
, где 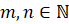 , называется обыкновенной дробью. Число
, называется обыкновенной дробью. Число 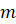 называется числителем дроби, число
называется числителем дроби, число 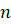 — знаменателем.
— знаменателем.
Дробь называется правильной, если её числитель меньше
знаменателя  , и неправильной, если её числитель больше знаменателя или
равен ему
, и неправильной, если её числитель больше знаменателя или
равен ему 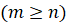 .
.
Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же число, не равное нулю, то получится дробь, равная данной.
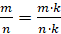 ,
, 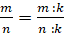
Число вида  , где
, где 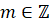 ,
, 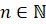 , называется рациональным. Множество рациональных чисел
обозначается
, называется рациональным. Множество рациональных чисел
обозначается 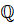 .
.
А теперь вспомним правила выполнения арифметических действий над рациональными числами:
1. Сложение рациональных чисел:

2. Вычитание рациональных чисел:

3. Умножение рациональных чисел:

4. Частное двух рациональных чисел:.

Десятичные дроби — это такие обыкновенные дроби, у которых знаменатель — единица с нулями, то есть 10; 100; 1000 и так далее.
Десятичные дроби записывают без знаменателей. Сначала пишут целую часть числа, справа от неё ставят запятую; первая цифра после запятой означает число десятых (то есть десятых долей единицы), вторая — сотых, третья — тысячных и так далее.

Цифры, стоящие после запятой, называются десятичными знаками.
Бесконечной называется десятичная дробь, у которой после запятой бесконечно много цифр.
Каждое рациональное число  может быть представлено в виде конечной или бесконечной десятичной
дроби. Это достигается делением числителя на знаменатель.
может быть представлено в виде конечной или бесконечной десятичной
дроби. Это достигается делением числителя на знаменатель.
Обыкновенная несократимая дробь  может быть записана конечной десятичной дробью тогда и только
тогда, когда её знаменатель не содержит никаких других простых множителей, кроме
2 или 5.
может быть записана конечной десятичной дробью тогда и только
тогда, когда её знаменатель не содержит никаких других простых множителей, кроме
2 или 5.
Бесконечную десятичную дробь называют периодической, если у неё, начиная с некоторого места, одна цифра или группа цифр повторяется, непосредственно следуя одна за другой. Повторяющуюся цифру или группу цифр называют периодом и записывают в скобках.
Например,  .
.
Если период начинается сразу после запятой, то дробь называют чисто периодической; если же между запятой и периодом есть другие десятичные знаки, то дробь называют смешанной периодической.
Правила обращения периодической дроби в обыкновенную:
1. Для обращения чистой периодической дроби в обыкновенную в числителе оставляют период десятичной дроби, а в знаменателе — число, состоящее из девяток, взятых столько раз, сколько знаков в периоде десятичной дроби.
Например:

2. Для обращения смешанной периодической десятичной дроби в обыкновенную в числителе берут число, стоящее в десятичной дроби до второго повторения периода, минус число, стоящее в десятичной дроби до периода; в знаменателе нужно написать столько девяток, сколько цифр в периоде, и приписать к ним столько нулей, сколько цифр в исходной десятичной дроби от запятой до периода.
Например:

Бесконечная десятичная непериодическая дробь называется иррациональным числом.
Рациональные и иррациональные числа образуют множество
действительных чисел. Множество действительных чисел обозначают заглавной
латинской буквой  .
.
Модулем (абсолютной величиной)
действительного числа  называют само это число
называют само это число  , если
, если  , и противоположное число
, и противоположное число  , если
, если  .
.

Геометрически модуль числа означает расстояние на координатной
прямой от точки  до точки
до точки  .
.

Модуль действительного числа обладает свойствами.
При  имеем:
имеем:
1.  тогда и только тогда, когда
тогда и только тогда, когда  или
или  ;
;
2.  тогда и только тогда, когда
тогда и только тогда, когда  ;
;
3.  тогда и только тогда, когда
тогда и только тогда, когда  или
или  .
.
Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.
Задание первое. Найдите значение
выражения  .
.
Решение.

Задание второе. Расположите в порядке возрастания числа:
 ;
;  ;
; 
 ;
;  ;
;  .
.
Решение.

Задание третье. Найдите целые числа  и
и  такие, что
такие, что  .
.
Решение.

Задание четвёртое. При каких
натуральных значениях 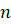 дробь
дробь  является целым числом?
является целым числом?
Решение.

Задание пятое. Укажите наибольшее
целок  , при котором дробь
, при котором дробь  является целым числом.
является целым числом.
Решение.


 Получите свидетельство
Получите свидетельство Вход
Вход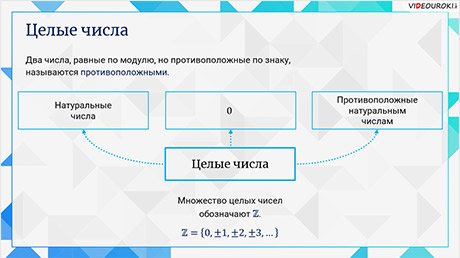




 8092
8092