Напомним, что понятие «натуральное число» является
первоначальным, неопределяемым. Оно возникло из потребностей счёта. Множество
натуральных чисел обозначают 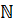 .
Наименьшее натуральное число —
.
Наименьшее натуральное число — 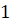 .
Наибольшего натурального числа нет. Для записи натуральных чисел используют
цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Нуль не является натуральным числом.
.
Наибольшего натурального числа нет. Для записи натуральных чисел используют
цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Нуль не является натуральным числом.
Число, например, состоящее из а сотен, b десятков и c единиц, записывается в виде:
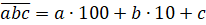 .
.
В следующей записи 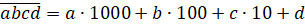 цифра
а показывает количество тысяч, b — количество сотен, b — количество десятков и
цифра
а показывает количество тысяч, b — количество сотен, b — количество десятков и 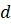 — количество
единиц в числе.
— количество
единиц в числе.
Вы уже знаете, что натуральные числа можно сравнивать между собой, складывать и умножать. Из большего натурального числа можно вычесть меньшее.
Если натуральное число 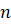 делится
на натуральное число
делится
на натуральное число 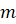 без
остатка, то есть
без
остатка, то есть 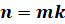 , где
, где  , то
число
, то
число 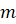 называют
делителем числа
называют
делителем числа 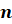 , а
число
, а
число 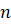 — кратным
числа
— кратным
числа 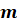 .
.
Вот такая запись 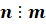 означает,
что
означает,
что 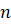 делится на
делится на 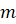 нацело.
нацело.
Натуральное число, не равное единице, называется простым, если оно имеет только два делителя: единицу и само это число.
Например: 2, 3, 5, 7, 11, 17 — простые числа.
Натуральное число называется составным, если оно имеет более двух делителей. Например: 6, 15, 24, 36 — составные числа.
Число 1 не является ни простым, ни составным. Простых чисел бесконечно много. Каждое составное число разлагается на простые множители и притом единственным образом.
Сформулируем признаки делимости натуральных чисел:
1. Для делимости на 2 нужно, чтобы последняя цифра числа была
чётная или 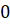 .
.
2. Для делимости на 3 нужно, чтобы сумма цифр числа делилась на 3.
3. Для делимости на 4 нужно, чтобы две последние цифры числа были 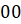 или
образовывали число, делящееся на 4.
или
образовывали число, делящееся на 4.
4. Для делимости на 5 нужно, чтобы последняя цифра числа была 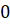 или
5.
или
5.
5. Для делимости на 8 нужно, чтобы три последние цифры числа были 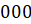 или образовывали
число, делящееся на 8.
или образовывали
число, делящееся на 8.
6. Для делимости на 9 нужно, чтобы сумма цифр числа делилась на 9.
7. Для делимости на 10 нужно, чтобы последняя цифра числа была 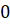 .
.
8. Для делимости на 11 нужно, чтобы разность между суммой цифр, стоящих на чётных местах, и суммой цифр, стоящих на нечётных местах, делилась на 11.
9. Для делимости на 25 нужно, чтобы две последние цифры числа были
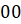 или
образовывали число (25, 50 или 75), делящееся на 25.
или
образовывали число (25, 50 или 75), делящееся на 25.
Наибольшее из натуральных чисел, на которое делятся числа 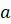 и
и 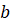 ,
называется их наибольшим общим делителем и обозначается НОД (
,
называется их наибольшим общим делителем и обозначается НОД (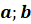 ).
).
Числа 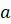 и
и 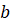 называются
взаимно обратными, если
называются
взаимно обратными, если 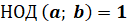 .
.
Наименьшее из натуральных чисел, которое делится на числа 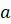 и
и 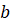 ,
называется их наименьшим общим кратным и обозначается
,
называется их наименьшим общим кратным и обозначается 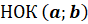 .
.
Разделить натуральное число 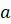 на
натуральное число
на
натуральное число 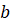 с
остатком – это значит представить
с
остатком – это значит представить 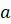 в
виде:
в
виде: 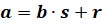 , где
, где 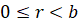 .
.
Например, 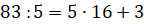 .
.
Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.
Задание первое. Найдите значение
выражения  .
.
Решение.
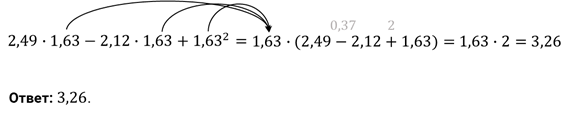
Задание второе. Найдите наибольшее натуральное число, которое при делении на 15 с остатком даёт частное, равное 19.
Решение.

Задание третье. Найдите все натуральные
числа вида 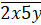 (здесь
(здесь
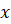 —
цифра сотен,
—
цифра сотен, 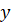 — цифра единиц), которые делятся на 12. В
ответ запишите их количество.
— цифра единиц), которые делятся на 12. В
ответ запишите их количество.
Решение.
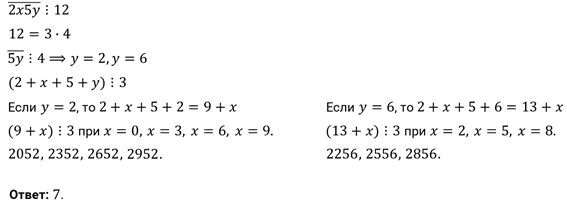
Задание четвёртое. Произведение двух чисел равно 10 800, а их НОД равен 60. Найдите НОК этих чисел.
Решение.
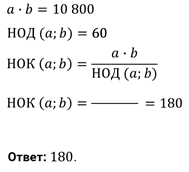
Задание пятое. Найдите все пары натуральных чисел, НОД которых равен 5, а НОК равно 105.
Решение.

Задание шестое. Сумма цифр искомого двузначного числа равна 8. Если цифры этого числа переставить, то получится число, которое меньше искомого на 18. Как велико искомое число?
Решение.

Задание седьмое. В двузначном числе цифра десятков на 4 больше цифры единиц. Когда это число разделили на цифру единиц, то в частном получилось 24, а в остатке число, которое на 2 меньше делителя. Найдите заданное число.
Решение.

Задание восьмое. В комнате стоят табуретки и стулья. У каждой табуретки по 3 ноги, у каждого стула по 4 ноги. Когда на всех табуретках и стульях сидят люди, то в комнате всего 39 ног. Сколько стульев и сколько табуреток в комнате?
Решение.

Задание девятое. Когда брату было столько лет, сколько сестре сейчас, им вместе было 15 лет; когда сестре будет столько лет, сколько сейчас брату, им вместе будет 27 лет. Найдите возрасты брата и сестры.
Решение.


 Получите свидетельство
Получите свидетельство Вход
Вход




 6517
6517