Признаки делимости на 9 и на 3

В математике существуют признаки делимости чисел. Это определённые правила, которые помогают по виду числа определить, делится ли оно на заданный делитель или нет.

Делимость чисел на 10, на 5 и на 2 зависит только от последней цифры. Напомним эти признаки.

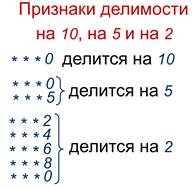
Если число оканчивается цифрой 0, то оно делится на 10 без остатка.

Если число оканчивается цифрами 0 или 5, то оно делится на 5 без остатка.

Если число оканчивается цифрами 2, 4, 6, 8 или 0, то оно делится на 2 без остатка.

А вот судить по последней цифре, делится ли число на 9 или на 3, нельзя. Хотя признак делимости на 9 существует.

Запишем ряд чисел, кратных 9.

По виду все числа разные, но это только на первый взгляд.

Заполним таблицу.

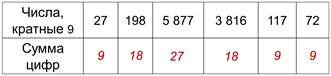
Если рассмотреть сумму цифр чисел, кратных 9, можно заметить, что сумма цифр тоже кратна 9, то есть делится на 9 без остатка.

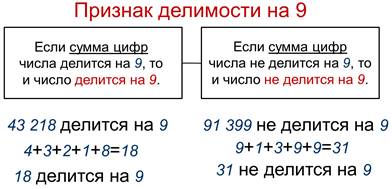
Итак, признак делимости на 9 звучит так:

Если сумма цифр числа делится на 9, то и число делится на 9; если сумма цифр числа НЕ делится на 9, то и число НЕ делится на 9.

Например

Если число большое, и сумма цифр числа получается тоже большая, не беда. Сложите цифры ещё раз. В этом случае судить о делимости на 9 будет проще.

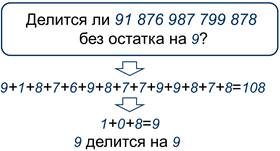
Поясним, почему делимость числа на 9 зависит только от суммы его цифр.

Например

Так рассуждать можно о делимости на 9 любого числа.

Кроме того, при нахождении чисел кратных девяти важно помнить таблицу умножения на 9. Для тех, кто ещё не выучил или уже забыл, предлагаем хороший способ запоминания.

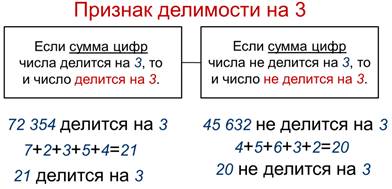
Для делителя 3 тоже существует признак делимости, очень похожий на признак делимости на 9:

Если сумма цифр числа делится на 3, то и число делится на 3; если сумма цифр числа НЕ делится на 3, то и число НЕ делится на 3.

Например

Задача

На день рождения детям подарили три одинаковых подарка. Может ли быть, что конфет во всех подарках было 35? 47? 111?

Итоги

Если сумма цифр числа делится на 9, то и число делится на 9 без остатка.

Если сумма цифр числа делится на 3, то и число делится на 3 без остатка.