Чтобы ответить на вопрос, делится ли одно число на другое без остатка, не всегда нужно выполнять деление. Для некоторых делителей есть способ более удобный: для них существуют признаки делимости.
Определение
Признак делимости — это правило, позволяющее сравнительно быстро определить, является ли число кратным заранее заданному.
А значит, изучив тему, мы сможем только по виду числа определять, делится ли оно на данное число или нет.
Начнем с числа 10. Выпишем ряд чисел, кратных 10.

Заметим, что все числа этого ряда оканчиваются цифрой нуль. Из этого можно сделать вывод:
Если запись натурального числа оканчивается цифрой 0, то это число делится без остатка на 10.
Если запись натурального числа оканчивается не цифрой 0, то это число не делится без остатка на 10.
Остаток в этом случае равен последней цифре числа.
Это правило называется признаком делимости на 10.
Повторим его ещё раз. Если запись натурального числа оканчивается цифрой 0, то это число делится без остатка на 10.
Если запись натурального числа оканчивается не цифрой 0, то это число не делится без остатка на 10.
Например

Теперь выпишем ряд чисел, кратных 5.

Заметим, что все числа этого ряда оканчиваются цифрой 5 или 0. Из этого можно сделать вывод:
Если запись натурального числа оканчивается цифрой 0 или 5, то это число делится без остатка на 5.
Все остальные числа на 5 не делятся без остатка.
Это правило называется признаком делимости на 5.
Повторим его ещё раз. Если запись натурального числа оканчивается цифрой 0 или 5, то это число делится без остатка на 5.
Если запись натурального числа оканчивается другой цифрой, то это число не делится без остатка на 5.
Например

Задача
В кошельке у Кати только пятирублевые монеты. Сможет ли она оплатить без сдачи в магазине торт за 125 рублей?

Поговорим о числе 2.
Определите, какое количество подарков принесут гости, если они пришли на день рождения к братьям близнецам?
Варианты: 9, 6, 13, 27.

Выпишем ряд чисел, кратных 2.

Заметим, что все числа этого ряда оканчиваются цифрами 2, 4, 6, 8, 0. Из этого можно сделать вывод:
Если запись натурального числа оканчивается цифрами 2, 4, 6, 8, 0, то это число делится без остатка на 2.
Все остальные числа на 2 не делятся без остатка.
Это правило называется признаком делимости на 2.
Повторим его ещё раз. Если запись натурального числа оканчивается цифрами 2, 4, 6, 8, 0, то это число делится без остатка на 2.
Если запись натурального числа оканчивается цифрами 1, 3, 5, 7 или 9, то это число не делится без остатка на 2.
Определение
Числа, кратные двум, называются чётными.
Числа, не кратные двум, называются нечётными.
Основоположниками теории делимости на 2 являются Пифагор и его ученики. Они разбили числа на чётные - «женские» и нечётные - «мужские». И когда пифагорейцы, по обычаю античных времён, приносили подношения высшим силам, богам выделялось нечётное количество предметов, а богиням - чётное.
Например

Теперь обоснуем признаки делимости на 10, на 5 и на 2.
Любое натуральное число а можно представить в виде суммы некоторого числа десятков и однозначного числа:

Например

В выражении d ∙ 10 + e

Чтобы всё число а делилось на 10, на 5 и на 2, нужно чтобы оба слагаемых делились на 10, 5 и 2. Первое слагаемое делится и на 10, на 5 и на 2. Значит, делимость зависит от второго слагаемого, т.е. от последней цифры числа.

Итоги
Таким образом,
Если запись натурального числа оканчивается цифрой 0, то это число делится без остатка на 10.
Если запись натурального числа оканчивается цифрой 0 или 5, то это число делится без остатка на 5.
Если запись натурального числа оканчивается цифрами 2, 4, 6, 8, 0, то это число делится без остатка на 2.
Эти правила называются признаками делимости.

 Получите свидетельство
Получите свидетельство Вход
Вход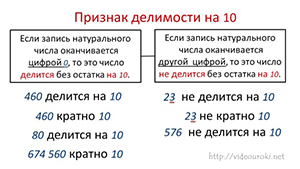



 0
0 9015
9015


