Делители и кратные

Поговорим о действии деления.

Определение

Деление – это действие разложения величины на равные части.

Например

6 яблок разделить поровну на двоих детей.

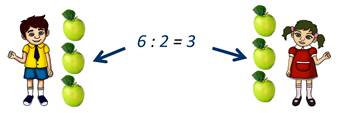
Конечно, и 5 яблок можно поделить между двумя детьми, но для этого придётся одно из яблок разрезать пополам.

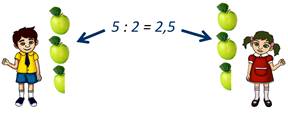
Возможно и деление с остатком.

Сегодня мы рассмотрим деление натуральных чисел, когда числа делятся без остатка.

Пример

На день рождения Маша получила 8 воздушных шаров. Она решила поделиться со своей подругой Леной и пригласила её в гости.

«Нам двоим достанется по 4 шарика», - подумала Маша.

Но праздник был бы не таким веселым, если бы в гости не заглянул друг Коля.

«Как же теперь делить воздушные шары?» - подумала Лена.

8 шариков не разделишь поровну на трёх друзей. Ведь воздушные шары не яблоки, их не разрежешь на части.

Но Коля пришёл не один, а вместе с братом Ваней.

«Ну, что ж, проблема решена, - подумала именинница, – теперь каждому из нас достанется по 2 шарика».

Рассмотрим данный пример с математической точки зрения.

Определение

Делителем b натурального числа а называют натуральное число b, на которое а делится без остатка.

Важно понимать различие понятия делится от понятия делить.

Задание

Найти все делители числа 12.

Ещё одним важным понятием темы будет понятие «кратное».

В примере с шариками:

Например

Все эти числа делятся на 7.

Пример

В пачке по 10 печений. Не раскрывая пачек, можно взять 10 печений, 20 печений, 30 печений.

А вот 23 печенья взять нельзя.

Говорят, числа кратные 10 это 10, 20, 30. Число 23 не кратно числу 10.

Определение

Если натуральное числа а делится на натуральное число b, то число а называют кратным числа b.

Другими словами, число а кратно числу b – значит а делится на b.

Теперь поговорим о количестве делителей и кратных.

Для числа 10 делителей будет 4: 1, 2, 5 и 10.

Теперь запишем кратные 10: 10, 20, 30, 100, 1000. Все числа и не запишешь.

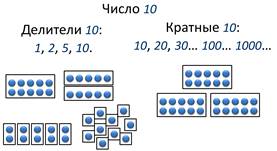
Запомним, любое натуральное число имеет бесконечно много кратных и ограниченное число делителей.

Итоги

8 делится на 2. Можно сказать: «2 делитель восьми» или «8 кратно 2».

Делителей всегда конечное множество, т.е. мы можем перечислить все делители. А вот количество кратных бесконечно.