Пример.
Пусть имеются 5 цветков различного цвета. Для удобств обозначим их буквами: A, B, C, D, E. Составить букеты из трёх цветков.
Если в букет входит цветок А, то можем составить такие букеты:
ABC, ABD, ABE, ACD, ACE и ADE.
Если в букет входит цветок B, но не входит А, то составим букеты:
BCD, BCE и BDE.
Если же в букет входит цветок C и не входят А и B, то получим только один букет: CDE.
Мы составили все возможные сочетания из 5 элементов по 3.
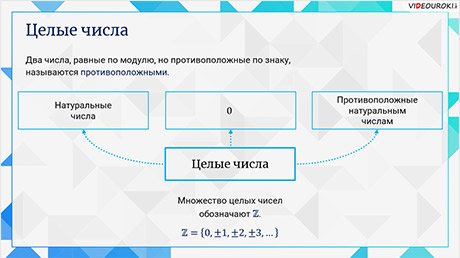
Определение:
Сочетанием
из n
элементов по k
называется любое множество, составленное из k элементов, выбранных из данных n элементов. Обозначают 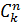 .
.
В отличие от размещений в сочетаниях не имеет значения, в каком порядке расположены элементы. Сочетания считаются различными, если они отличаются хотя бы одним элементом.
Например:

Эти два букета являются размещениями, так как в их состав входят одни и те же элементы, только с разным расположением.

А два таких букета являются сочетаниями, ведь они отличаются составом элементов.
Мы составили все сочетания из 5 элементов по 3, и выяснили, что:
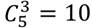
Выведем формулу из n сочетаний по k. Допустим, что имеется множество из n элементов, и из них составлены все возможные сочетания по k элементов. Число таких сочетаний равно:
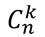
В
каждом из этих сочетаний можно выполнить 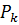 перестановок.
В результате мы получим все размещения, которые можно получить из n элементов
по k:
перестановок.
В результате мы получим все размещения, которые можно получить из n элементов
по k:
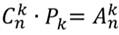
Пользуясь уже известными формулами числа перестановок и размещений, получим такое равенство.
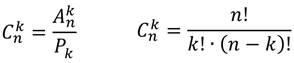
Получили формулу нахождения числа сочетаний из n элементов по k. При этом k≤n.
Пример.
1. Найти число сочетаний из 7 элементов по 4.
Запишем:
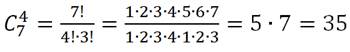
2. Вычислим число сочетаний из 10 элементов по 5:
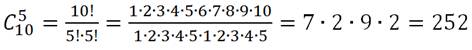
3. Найти число сочетаний из 15 элементов по 2:
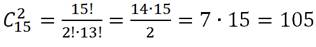
Пример.
Турист запланировал взять с собой в поездку 8 футболок, при этом всего их у него насчитывается 12. Сколькими способами он может сделать выбор?
Применим формулу:
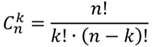
У вас мог возникнуть вопрос, почему мы не ищем число размещений?
Но вспомнив отличие размещений от сочетаний, становиться ясно, что туристу не важно, в каком порядке он соберёт футболки. Ему важно, какие именно из них он возьмёт с собой.
Найдем число сочетаний:
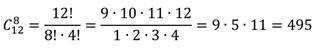
Пример.
В чемпионате принимало участие 8 команд. Каждая команда сыграла с каждой только 1 раз. Сколько всего было игр?
То есть нужно выяснить, сколько различных по составу пар можно получить из 8 элементов.
Найдём число сочетаний:
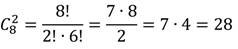
Получили, что всего было 28 игр.
Пример.
Найти сколькими способами для участия в конкурсе можно выбрать 2 мальчика и 4 девочки, если в классе 11 мальчиков и 13 девочек?
Для начала выясним, сколькими способами можно выбрать мальчиков. Всего мальчиков 11, а выбрать нужно 2.
Число
возможных вариантов выбора мальчиков равно 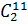 ,
а для выбора девочек нужно
,
а для выбора девочек нужно 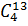 .
.
Общее число способов:



Получили 39325 способов.

 Получите свидетельство
Получите свидетельство Вход
Вход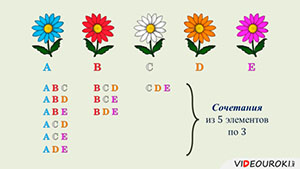



 0
0 8356
8356