Теория вероятностей - это раздел математики, который изучает закономерности случайных событий.
События можно считать случайными - это те, которые могут произойти, а могут и не произойти.
Примерами таких событий являются: выпадение орла или решки при подбрасывании монеты; поражение мишени или промах при стрельбе; выпадение того или иного количества очков при бросании игрального кубика.
Пример.
Провели испытания. 100 раз бросали игральный кубик и подсчитали, что 6 очков выпало 17 раз - частота рассматриваемого события, то есть выпадения очков.
Отношение частоты к общему числу испытаний называют относительной частотой этого события.
Пусть некоторое испытание проводилось многократно в одних и тех же условиях. При этом фиксировалось, произошло или нет некоторое интересующее нас событие А.
Если общее число испытаний - n, а число испытаний, при которых произошло событие А, - m. То m называют частотой события А, частное m и n - относительной частотой.
Определение:
Относительной частотой случайного события в серии испытаний называется отношение числа испытаний, в которых это событие наступило, к числу всех испытаний.
В ходе исследований выяснилось, что относительная частота появления ожидаемого события при повторении опытов в одних и тех же условиях, может оставаться примерно одинаковой, незначительно отличаясь от некоторого числа р.
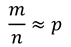
Пример.
При подбрасывании монеты отмечают те случаи, когда выпадает орёл.
Если монета однородна и имеет правильную геометрическую форму, то шансы выпадения орла или решки будут примерно одинаковы. Но при небольшом количестве бросков такой результат может не получиться.
А вот если испытание проводиться большое количество раз, то относительная частота выпадения орла близка к относительной частоте выпадения решки.
Многие учёные проводили такой эксперимент.
Так, например, английский математик Карл Пирсон бросал монету 24 тысячи раз, и относительная частота выпадения орла оказалось равной 0,5005.
А наш соотечественник, Всеволод Иванович Романовский, подбрасывая монету 80 тысяч 640 раз, нашёл, что относительная частота выпадения орла в его испытании была равна 0,4923.
Заметим,
что в обоих случаях относительная частота выпадения орла очень близка к  .
.
Говорят,
что вероятность выпадения орла при подбрасывании монеты правильной
геометрической формы равна  .
.
Пример.
В непрозрачном мешке лежит 7 зелёных и 12 синих кубиков. За раз можно доставать только 1 из них. Какова вероятность того, что из мешка достанут синий кубик?
Всего в мешке 19 кубиков. Значит, n=19.
Синий кубик мы можем достать 12 раз. Получаем, что m=12.
Относительная частота равна:
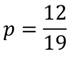
Вероятность
того, что из мешка достанут синий кубик, равна 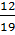 .
.
Пример.
Определить относительную частоту появления буквы «о» в слове «достопримечательность».
Общее число букв, то есть n=21. А количество букв «о», то есть m=3.
Значит относительная частота:
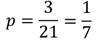
Пример.
Отмечая число попаданий в корзину в каждой серии из 40 бросков, которые совершал баскетболист, получили такие данные:
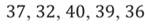
Какова относительная вероятность попадания мяча в корзину для данного баскетболиста?
Определим общее число бросков. Было 5 серий по 40 бросков, то есть n=200.
Сосчитаем число попаданий в корзину:
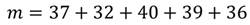
Получили, что m=184.
Относительная вероятность попадания в корзину будет:
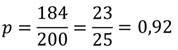
Пример.
Стрелок совершил 50 выстрелов. Относительная частота попадания в цель оказалась равной 0,88. Сколько раз он промахнулся?
Зная общее число выстрелов n=50 и относительную вероятность попадания p=0,88. Найдем число попаданий в цель:

Стрелок попал в цель 44 раза.
Найдём число промахов

Стрелок промахнулся 6 раз.

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 17544
17544

