Пример.
Пусть имеются 4 шара и 3 пустые ячейки. В каждую ячейку можно поместить только по 1 шару.
Для удобства обозначим шары буквами: A, B, C, D.
Если поместим шар А в первую ячейку, шар B - во вторую ячейку, а шар C - в третью, то мы получим одну из возможных упорядоченных троек шаров.
Выбирая по-разному шары для каждой из ячеек, получим, например, такие тройки:

Каждую такую упорядоченную тройку, составленную из четырёх элементов, называют размещением из 4 - х элементов по 3.
Определение:
Размещением из n элементов по k, где k≤n, называется любое множество, состоящее из k элементов, взятых в определённом порядке из данных n элементов.
Два размещения из n элементов по k считаются различными, если они различаются самими элементами или порядком их следования.
Обозначают:
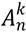
Вернемся к примеру, вычислим количество таких размещений для данного случая, пользуясь правилом комбинаторного умножения:
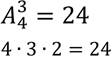
Получим формулу для вычисления числа размещений из n элементов по k:
Для выбора первого элемента можно взять любой из n элементов, то есть существует n способов. Для выбора второго элемента можем взять любой из n-1 оставшихся элементов, то есть n-1 способов. Третий элемент можно выбрать n-2 способами. И так далее.
Так k - ый элемент можно выбрать n-(k-1) способами.
Число размещений из n элементов по k можно отыскать по такой формуле:
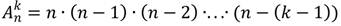
Преобразуем, умножим и разделим правую часть этого равенства:
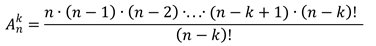
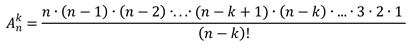
Тогда формула числа размещений из n элементов по k примет такой вид:
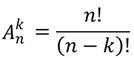
Стоит обратить внимание на то, что размещения из n элементов по n отличаются только порядком следования элементов, так как каждый из них должен участвовать в размещении.
Тогда получаем, что такое размещение является перестановкой.
Пример.
1. Вычислить число размещений из 5 элементов по 3.
Воспользовавшись формулой размещений, получим:
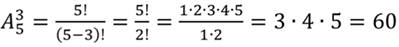
2. Вычислим:
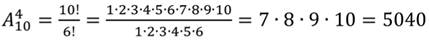
3. Вычислим:
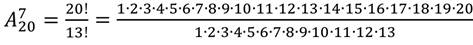
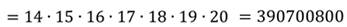
4. Вычислить:
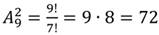
Пример.
Девять карточек пронумерованы цифрами 1, 2, 3, 4, 5, 6, 7, 8, 9. Из этих карточек 4 наугад выкладывают в ряд. Сколько при этом различных 4 - ых чисел можно получить?
Суть задачи состоит в том, что из 9 данных цифр нужно составить всевозможные 4 - ые числа, не повторяя цифры в числе.
Найдем число размещений:
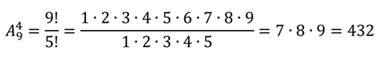
Пример.
В классе 17 учеников, а на скамейке в парке помещается только 5 человек. Сколькими способами одноклассников можно усадить на скамейку в парке? Порядок рассадки имеет значение.
Найдем количество размещений:

Пример.
Сколько можно составить телефонных номеров, из 6 цифр каждый, так чтобы все цифры были различны? При этом на первом месте не могут быть цифры 0 и 1.
У
нас есть 10 различных цифр. Из них можно составить 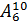 комбинаций телефонных номеров.
комбинаций телефонных номеров.
Но
на первом месте не может быть цифра 0. Зафиксируем её на первом месте. В нашем
распоряжении осталось 9 цифр и мы размещаем их на 5
позициях. Получаем, что количество номеров начинающихся на нуль -  .
Количество номеров, начинающихся единицей -
.
Количество номеров, начинающихся единицей - 
Получим:

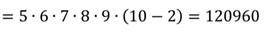
Можно составить 120960 телефонных номеров, состоящих из 6 цифр и не начинающихся 0 и 1.

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 8088
8088

