Вспомогательные алгоритмы и подпрограммы: функции

Вопросы:

·     Определение функции.

·     Описание и вызов функций.

·     Применение функций при написании программ.

Функцией называется подпрограмма, которая при выполнении принимает на вход любое количество параметров, а по завершении работы возвращает одно значение заданного типа, содержащееся в переменной, название которой совпадает с названием функции.

В программах на языке Pascal, функции, как и процедуры, описываются в разделе описания подпрограмм. Описание функции начинается со служебного слова function. После него, через пробел, следует имя функции, которое не должно совпадать с именем программы или с именами переменных. После него через пробел в скобках следует описание формальных параметров, которые оформляются, как и в процедуре. Сначала через запятую перечисляются параметры-значения одного типа. Через двоеточие после них указывается тип параметров. Параметры разных типов разделяются точкой с запятой. Дальше со служебного слова var начинается описание параметров-переменных. Они описываются также, как и параметры-значения. После описания формальных параметров через двоеточие указывается тип значения, возвращаемого функцией. После него следует точка с запятой. На следующей строке, если нужны дополнительные переменные, следует раздел описания промежуточных параметров функции. Дальше, между логическими скобками, следует блок операторов функции. После служебного слова end следует точка с запятой.

Важно: в программном блоке функции, переменной, название которой соответствует названию функции, хотя бы один раз должно быть присвоено какое-либо значение.

function <имя> (<параметры-значения>: <тип>; var <параметры-переменные>: <тип>): <тип значения>;

var

  <дополнительные параметры>;

begin

  <оператор 1>;

  <оператор 2>;

  …

  <имя>:=<выражение>;

  …

  <оператор n>;

end;

Описание функции

Так же, как и процедура, функция может не иметь формальных параметров, если все входные данные задаются через глобальные параметры.

Вызов функции в операторном блоке программы происходит лишь в составе какого-либо оператора. При этом указывается имя функции, после которого, в скобках, следуют её фактические параметры. При вызове функции, также как и в случае с процедурой, важно чтобы количество, порядок следования и тип её фактических параметров совпадали с формальными параметрами в её описании.

t:=<имя> (<фактические параметры>);

Вызов функции

При выполнении программы, в которой содержится функция, выполняются сначала операторы, следующие до содержащего вызов функции. При выполнении этого оператора вычисляется значение функции. Для этого фактические параметры, указанные при вызове, подставляются на места формальных параметров, указанных в описании функции. После этого выполняются операторы, содержащиеся в её операторном блоке. Так как в операторном блоке функции, переменной соответствующей функции присваивается какое-либо значение, это значение подставляется в оператор содержащий вызов функции. После чего его выполнение завершается и начинают выполняться операторы, следующие в теле программы после него.

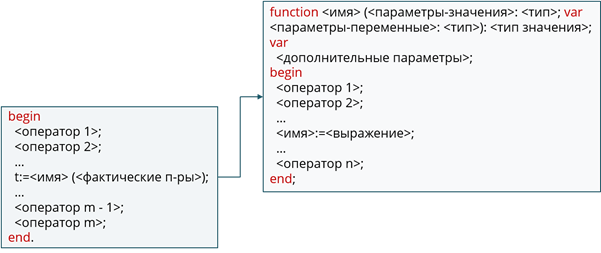
Принцип работы вызова функции

Задача: Написать программу, которая определяет является ли целое n, заданное пользователем, простым числом Мерсенна. 4 ≤ n ≤ 2 000 000 000.

Числами Мерсенна называются числа вида 2^p – 1. Числа Мерсенна названы так в честь французского математика Марена Мерсенна, который изучал эти числа. Он также являлся учителем Блеза Паскаля, в честь которого назван изучаемый нами язык программирования.

Марен Мерсенн

(1588–1648)

Простыми числами Мерсенна называются числа Мерсенна, которые являются простыми и у которых p – также простое число. Простым называется число, которое не делится нацело ни на одно число кроме единицы и себя самого.

Данную задачу можно разделить на две подзадачи: в начале определим является ли заданное n числом Мерсенна. Если это число Мерсенна – определим является ли оно простым.  Однако первую подзадачу можно также разбить на две подзадачи. Сначала мы должны определить, можно ли представить число n + 1 в виде 2^p. Если число можно представить в указанной форме, то нам остаётся определить не делится ли n на какое-нибудь число кроме 1 и себя самого. Для решения этой подзадачи мы опишем логическую функцию prost. Для решения первой подзадачи мы опишем логическую функцию, которую назовём Mersenn.

Декомпозиция задачи

Начнём написание программы для решения этой задачи. Назовём её число Мерсенна. Для решения задачи нам понадобится переменная для хранения числа n. По условию задачи, это число будет принимать значение на промежутке от 4 до 2 000 000 000, поэтому зададим его принадлежащим к целочисленному типу integer. Запишем логические скобки. Тело программы будет начинаться с оператора writeln, выводящего на экран сообщение о том, что это программа, определяющая, является ли целое n простым числом Мерсена. Дальше будет следовать оператор write с запросом на ввод n и оператор readln для его считывания. Для определения истинности высказывания о том, является ли n числом Мерсена, мы позже опишем логическую функцию Mersenn. Поэтому сейчас запишем условный оператор, условием которого будет значение этой функции, с параметром n. После служебного слова then в нём будет следовать ещё один условный оператор, который будет проверять, является ли n простым числом. Для определения истинности высказывания об этом мы позже опишем логическую функцию prost. В качестве условия укажем её значение также с параметром n. В этом условном операторе, после слова then запишем оператор write, который выводит на экран сообщение о том, что заданное n является простым числом Мерсенна. После служебного слова else запишем такой же оператор вывода, выводящий сообщение о том, что заданное n не является простым числом Мерсенна. Запишем служебное слово else для внешнего условного оператора. После него будет следовать такой же оператор вывода, как и предыдущий, поэтому просто скопируем его. На этом мы завершили описание основной программы.

program chislo_Mersenna;

var

 n: integer;

begin

 writeln ('Программа, определяющая, является ли целое n простым числом Мерсенна.');

 write ('n=');

 readln (n);

 if Mersenn (n)

 then if prost (n)

  then write (n, ' является простым числом Мерсенна.')

  else write (n, ' не является простым числом Мерсенна.')

 else write (n, ' не является простым числом Мерсенна.');

end.

Заголовок, переменные и операторный блок основной программы

Теперь опишем функцию определения истинности высказывания о том, что n является числом Мерсенна. Как мы помним, мы назвали её Mersenn, и она будет иметь один формальный параметр, назовём его также n. Как и в основной программе оно будет целочисленного типа integer. Так же нам потребуется промежуточная переменная p, которая будет хранить степень двойки в указанном представлении числа n, поэтому для её хранения нам будет достаточно целочисленного типа byte. Напишем логические скобки. Сначала для удобства расчёта p увеличим значение n на 1.  Присвоим переменной p значение ноль, так как мы её ещё не рассчитывали. Затем запишем оператор цикла с предусловием while. Его условием будет: n mod 2 = 0. В самом цикле мы будем значение переменной p увеличивать на 1, а n делить без остатка на 2. Таким образом, по окончании работы цикла, если n будет равно единице, то его удалось представить в виде 2^p, в противном случае этого сделать нельзя. Запишем условный оператор, который проверяет равно ли n единице, если это так – присвоим переменной Mersenn значение true. В противном случае запишем оператор присваивания переменной Mersenn значения false. На этом описание функции Mersenn будет завершено.

function Mersenn (n: integer): boolean;

begin

 n:=n+1;

 while n mod 2=0 do

  n:=n div 2;

 if n=1

 then Mersenn:=true

 else Mersenn:=false;

end;

Функция Mersenn

Теперь разберёмся, как определить является ли целое число n простым. Так как простым является число, которое не делится ни на одно целое число кроме 1 и себя самого, нам достаточно проверить делимость числа n на все числа на промежутке от 2 до n – 1. Но этот промежуток можно сократить. Очевидно, что

n =  * ,

следовательно, если при разложении n на два множителя один из них будет больше 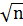, то второй будет меньше его. Значит нам достаточно проверить делимость n на все числа до 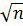. Так же мы можем, единожды проверив делимость n на 2, больше не проверять его делимость на чётные числа, так как если хотя бы один из делителей числа является чётным, то и само число должно быть чётным. И наконец, если мы нашли хотя бы один делитель числа Эн проверку можно остановить.

Опишем логическую функцию проверки того, является ли число n простым. Мы назвали функцию prost. Так как функция Mersenn содержит вызов функции prost, то она должна находится выше. У неё будет всего один аргумент – число n. Как и в основной программе зададим его принадлежащим к типу integer. Сама же функция будет логического типа boolean. Так же нам понадобится промежуточная переменная, в которой бы будем перебирать множители, назовём её i. Она так же будет принадлежать к типу integer, и ещё одна промежуточная логическая переменная – t. Запишем операторный блок функции. Он будет начинаться с того, что мы проверим не делится ли n без остатка на 2 и результат присвоим переменной t. Так как мы проверили делимость n на 2 – присвоим переменной i значение следующего предполагаемого делителя, то есть 3. Дальше запишем оператор цикла с предусловием while с условием продолжения работы: i <= sqrt (n). Так как функция извлечения квадратного корня sqrt является вещественной, то при расчёте результата возможна погрешность, поэтому добавим к sqrt (n) единицу. Второй частью условия продолжения работы цикла будет то, что t = true, то есть что мы ещё не нашли ни одного делителя n. В теле цикла будет больше одного оператора, поэтому напишем логические скобки. В цикле мы сначала запишем условный оператор с условием: n mod i = 0. Если это условие выполняется, то i является делителем n, а значит n не является простым числом и мы присвоим переменной t значение false. После проверки мы увеличим значение i на 2, чтобы пропустить чётное число, и перейти сразу к следующему за ним нечётному числу. Таким образом по завершении работы цикла переменная t будет содержать значение истинности высказывания о том, что число n является простым. Присвоим это значение переменной функции prost. На этом работа функции будет завершена.

function prost (n: integer): boolean;

var

 i: integer;

 t: boolean;

begin

 t:=n mod 2<>0;

 i:=3;

 while (i<=sqrt(n)+1) and (t=true) do

 begin

  if n mod i=0

  then t:=false;

  i:=i+2;

 end;

 prost:=t;

end;

Функция prost

Запустим программу на выполнение. Введём n = 524 287. Заданное число действительно является простым числом Мерсенна.

Снова запустим программу и зададим n = 2047. Это число не является простым числом, а значит и не является простым числом Мерсенна.

Программа работает правильно. Задача решена.

Важно запомнить:

Функции – это подпрограммы, которые в ходе исполнения принимают на вход некоторый набор параметров, а по завершении работы возвращают всего один простой параметр, содержащийся в переменной, имя которой совпадает с именем функции.

Описание функции:

function <имя> (<параметры-значения>: <тип>; var <параметры-переменные>: <тип>): <тип значения>;

var

  <дополнительные параметры>;

begin

  <оператор 1>;

  <оператор 2>;

  …

  <имя>:=<выражение>;

  …

  <оператор n>;

end;

Вызов функции:

t:=<имя> (<фактические параметры>);