Вопросы:
· Вспомогательные алгоритмы.
· Подпрограммы.
· Применение процедур при написании программ.
Ранее мы изучили этапы разработки программы для решения задачи. Одним из таких этапов является построение алгоритма. Однако, в случае если задача сложная, то и алгоритм её решения сразу придумать сложно. Для того, чтобы облегчить построение алгоритма, задачу можно разбить на несколько, более простых, подзадач. Каждую из них можно решить по отдельности. Алгоритмы решения этих подзадач будут частями алгоритма решения исходной задачи. Каждая такая часть алгоритма называется вспомогательным алгоритмом.
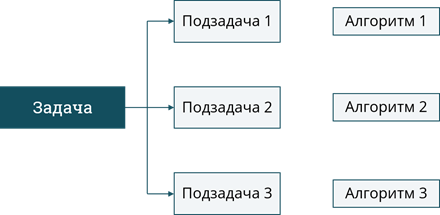
При программировании вспомогательные алгоритмы оформляются в виде подпрограмм. Это обеспечивает возможность повторного использования таких алгоритмов. Например, единожды написав подпрограмму для нахождения расстояния между двумя точками, её можно использовать в задаче для нахождения периметра многоугольника, заданного своими вершинами.
В языке программирования Pascal есть 2 вида подпрограмм: процедуры и функции. Сегодня мы рассмотрим процедуры. Процедурой называется подпрограмма, которая при выполнении принимает на ввод любое количество параметров, и по завершении работы возвращает также любое количество параметров.
В программах на языке Pascal, и процедуры и функции оформляются в разделе описания подпрограмм. Он размещается между разделом описания переменных и блоком операторов. Запись процедуры начинается со служебного слова procedure. После него через пробел следует имя процедуры. Оно не должно совпадать с именем программы или с именами переменных. После него через пробел в скобках следует описание формальных параметров. Оно начинается с описания параметров-значений, которые являются входными данными процедуры. Сначала через запятую перечисляются параметры одного типа. После них через двоеточие указывается тип параметров. Параметры разных типов разделяются точкой с запятой. Дальше со служебного слова var начинается описание параметров-переменных, которые являются выходными данными процедуры. Параметры-переменные описываются также, как и параметры-значения. После описания формальных параметров следует точка с запятой. На следующей строке, если нужны дополнительные переменные, следует раздел описания промежуточных параметров процедуры, который оформляется как раздел описания переменных в программе. Дальше между логическими скобками следует блок операторов процедуры. После служебного слова end следует точка с запятой.
procedure <имя> (<параметры-значения>: <тип>; var <параметры-переменные>:<тип>);
var
<дополнительные параметры>: <тип>;
begin
<оператор 1>;
<оператор 2>;
…
<оператор n>;
end;
Описание процедуры
Вызов процедуры в операторном блоке программы происходит следующим образом: сначала указывается имя процедуры, после которого в скобках следует перечисление фактических параметров процедуры. После скобок следует точка с запятой. Важно чтобы количество, порядок следования и тип фактических параметров при вызове процедуры совпадали с формальными параметрами в её описании.
<имя> (<фактические параметры>);
Вызов процедуры
При выполнении программы в которой содержится процедура выполняются сначала операторы, следующие в теле программы до вызова процедуры. При вызове процедуры фактические параметры, подставляются на места формальных параметров в её описании. После этого выполняются операторы, содержащиеся в операторном блоке процедуры. Дальше значения операторов-переменных, вычисленных при выполнении процедуры, подставляются в соответствующие им фактические параметры. После чего выполнение программы продолжается.
Важно понимать, что областью действия параметров, описанных в подпрограмме, является сама подпрограмма. Так переменные, описанные в подпрограмме, называются локальными переменными для этой подпрограммы. Переменные, описанные во внешней программе, называются глобальными по отношению к подпрограмме. Подпрограмма может обращаться к своим локальным и глобальным параметрам, но при этом внешняя программа не может обращаться к параметрам подпрограммы.
Задача: Даны 2 прямые на координатной плоскости, не совпадающие друг с другом и не параллельные оси y. Каждая из них задана координатами 2 точек, лежащих на ней. Найти координаты точки пересечения этих прямых. Если прямые параллельны друг другу – вывести сообщение об этом.
Данную задачу можно разделить на 3 подзадачи: в начале нужно, определить уравнения прямых по 2 точкам, которые на них лежат. Дальше нам нужно по уравнениям определить, являются ли заданные прямые параллельными. Если прямые не являются параллельными, то нужно вычислить координаты точки их пересечения. Так как выполнение первой подзадачи будет одинаковым для обеих прямых, оформим его в виде процедуры.
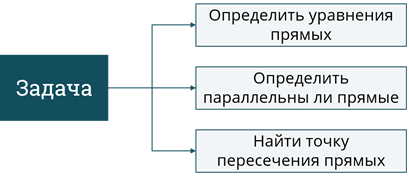
Декомпозиция задачи
Давайте разберёмся, как вывести уравнение прямой если она задана 2 точками. Как мы помним уравнение прямой на плоскости имеет вид y = kx + b, где x и y – это координаты любой точки, принадлежащей этой прямой. Подставив в это уравнение координаты двух точек, которыми задана прямая, мы получим два уравнения, составляющих систему.
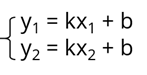
Нам остаётся лишь решить эту систему уравнений. Перенесём в обоих уравнениях первое слагаемое из правой части в левую часть. Мы получили что в правой части обоих уравнений остался только коэффициент b. Таким образом очевидно, что левые части этих уравнений равны между собой.
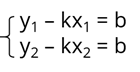
y1 – kx1 = y2 – kx2
В полученном уравнении сгруппируем слагаемые с коэффициентом k в левой части, а слагаемые без него – в правой части.
kx1 – kx2 = y2 – y1
В левой части полученного уравнения вынесем множитель k за скобки, после чего выражение в скобках перенесём в правую часть. Таким образом, мы получили:
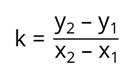
Для того, чтобы вычислить коэффициент b нам достаточно подставить в любое из двух ранее полученных уравнений коэффициент k.
b = y1 – kx1
Теперь мы знаем, как вычислить коэффициенты уравнения прямой.
Получив уравнения для обеих прямых, мы можем определить параллельны ли они друг другу. Как мы помним, коэффициент k в уравнении прямой равен тангенсу угла её наклона. Таким образом, если коэффициенты k этих уравнений совпадают, то они имеют одинаковый угол наклона, а значит они параллельны друг другу.
Если же прямые не параллельны, мы должны найти точку их пересечения. Решение этой подзадачи при написании программы мы также оформим в виде процедуры. Так как эта точка будет принадлежать обеим прямым, для её нахождения нужно лишь решить систему, состоящую из двух полученных нами уравнений прямых.
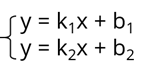
Так как левые части этих уравнений совпадают, то их правые части равны друг другу.
k1x + b1 = k2x + b2
В полученном уравнении в левой части сгруппируем слагаемые, содержащие координату x, а в правой части – оставшиеся 2 слагаемых.
k1x – k2x = b2 – b1
В левой части вынесем за скобки множитель x, после чего выражение в скобках перенесём в правую часть. Таким образом, мы получим:
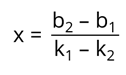
Для вычисления координаты y, подставим полученное значение x в одно из уравнений прямых.
y = k1x + b1
Напишем программу для решения задачи. Назовём её tochka. Для работы программы нам потребуются переменные, которые будут хранить координаты точек, задающих прямые: x1_1, x1_2, x2_1, x2_2, y1_1, y1_2, y2_1, y1_2. Также нам понадобятся переменные, которые будут хранить коэффициенты уравнений прямых: k1, k2 и b1, b2 и переменные для координат точки пересечения прямых: x и y. Так как в условии не сказано, что они целые, объявим их вещественного типа real.
Напишем логические скобки. В начале тела программы будет следовать оператор writeln, выводящий на экран сообщение о том, что это программа поиска точки пересечения прямых. Дальше напишем ещё один оператор writeln с запросом на ввод координат точек задающих первую прямую. Дальше будет следовать оператор write с запросом на ввод x1_1 и оператор readln, считывающий значение этой координаты. Теперь скопируем последние два оператора и изменим их для переменной y1_1. Затем скопируем последние четыре оператора и изменим их для координат второй точки. Теперь скопируем последние девять операторов и изменим их для ввода координат точек, задающих вторую прямую. Вызовем процедуру вычисления коэффициентов уравнения прямой – line, которую мы реализуем позже. Её входными параметрами будут координаты точек x1_1, y1_1, x1_2 и y1_2. Выходными параметрами будут коэффициенты уравнения первой прямой: k1 и b1. Снова вызовем эту же процедуру для вычисления коэффициентов уравнения второй прямой. Теперь запишем условный оператор, который будет проверять равны ли коэффициенты уравнений прямых k1 и k2. После слова then в этом условном операторе напишем оператор write, выводящий сообщение о том, что заданные прямые параллельны друг другу. После служебного слова else будет следовать несколько операторов, поэтому запишем логические скобки. Чтобы найти точку пересечения прямых вызовем процедуру point без параметров, которую мы опишем позже. После того, как мы вычислили координаты точки пересечения прямых запишем оператор write, выводящий на экран сообщение о том, что заданные прямые пересекаются в точке с координатами x и y.
program tochka;
var
x1_1, x1_2, x2_1, x2_2, y1_1, y1_2, y2_1, y2_2, k1, k2, b1, b2, x, y: real;
begin
writeln ('Программа поиска точки пересечения прямых.');
writeln ('Введите координаты точек, задающих первую прямую.');
write ('x1_1=');
readln (x1_1);
write ('y1_1=');
readln (y1_1);
write ('x1_2=');
readln (x1_2);
write ('y1_2=');
readln (y1_2);
writeln ('Введите координаты точек, задающих вторую прямую.');
write ('x2_1=');
readln (x2_1);
write ('y2_1=');
readln (y2_1);
write ('x2_2=');
readln (x2_2);
write ('y2_2=');
readln (y2_2);
line (x1_1, y1_1, x1_2, y1_2, k1, b1);
line (x2_1, y2_1, x2_2, y2_2, k2, b2);
if k1=k2
then write ('Заданные прямые параллельны.')
else begin
point ();
write ('Заданные прямые пересекаются в точке (', x, '; ', y, ').');
end;
end.
Заголовок, переменные и операторный блок основной программы
Теперь опишем процедуры, которые мы использовали в программе. Начнём с процедуры вычисления коэффициентов уравнения прямой — line. Как мы помним, её входными параметрами являются координаты точек, которыми задана прямая. Обозначим их: x1, y1 и x2 и y2, как мы помним, все они принадлежат к вещественному типу real. Выходные параметры этой процедуры – коэффициенты уравнения прямой: k и b, так же вещественного типа. Запишем логические скобки операторного блока процедуры. Он будет начинаться с вычисления k:= (x2 – x1) / (y2 – y1). Теперь запишем оператор присваивания b:= y - k*x1. На этом процедура line завершит свою работу.
procedure line (x1, y1, x2, y2: real; var k, b: real);
begin
k:=(y2-y1)/(x2-x1);
b:=y1-k*x1;
end;
Процедура line
Теперь опишем процедуру вычисления координат точки пересечения двух прямых — point. Реализуем её так, чтобы она получала и возвращала данные через глобальные переменные. Запишем в логических скобках операторный блок процедуры. В его начале запишем оператор присваивания x:= (b2 – b1) / (k1 – k2). После этого переменной y присвоим значение k1 * x + b1. На этом работа этой процедуры будет закончена.
procedure point ();
begin
x:=(b2-b1)/(k1-k2);
y:=k1*x+b1;
end;
Процедура point
Перейдём к тестированию программы. Запустив программу на выполнение, зададим сперва две параллельные прямые. Первую прямую зададим точками (7; 9) и (12; 11), а вторую прямую – точками (5; 4) и (0; 2). Программа действительно вывела сообщение о том, что заданные прямые параллельны.

Снова запустим программу на выполнение и зададим две прямые, которые пересекаются в точке (4; 4). Первую прямую зададим точками (2; 2) и (7; 7). Вторую прямую зададим точками (12; 4) и (1; 4). Программа действительно вывела сообщение о том, что заданные прямые пересекаются в точке (4; 4).

Программа работает правильно. Задача решена.
Обратим внимание на разницу в реализации процедур line и point. Чаще всего предпочтительнее первый вариант реализации, так как он более универсален, то есть такую процедуру можно легко использовать в другой программе или же несколько раз использовать для различных данных, так как мы делали в этой программе. Однако, когда в процедуру требуется передать большой объём данных может использоваться и передача через глобальные переменные, потому что такой способ передачи экономит оперативную память.
Важно запомнить:
· Вспомогательными алгоритмы – это, которые работают в составе других алгоритмов и используются для решения отдельных подзадач.
· Подпрограммы используются для записи вспомогательных алгоритмов при программировании.
· Процедуры и функции – это два вида подпрограмм в языке Паскаль. Они записываются между разделом описания переменных и операторным блоком программы.
· Процедуры могут принимать на вход и возвращать любое количество параметров.
Описание процедуры:
procedure <имя> (<параметры-значения>: <тип>; var <параметры-переменные>:<тип>);
var
<дополнительные параметры>: <тип>;
begin
<оператор 1>;
<оператор 2>;
…
<оператор n>;
end;
Вызов процедуры:
<имя> (<фактические параметры>);

 Получите свидетельство
Получите свидетельство Вход
Вход




 6730
6730

