Вопросы:
· Вложенные циклы.
· Итерационные циклы.
Начнём с вложенных циклов. Тело некоторых циклов может содержать в себе другие циклы. Циклы, которые располагаются внутри других циклов называются вложенными.
Задача: Совершенным называется число равное сумме своих делителей, с учётом 1, но без учёта самого числа. Написать программу, которая рассчитывает количество избыточных, недостаточных и совершенных чисел промежутке от 2 до n. n вводится с клавиатуры и находится на промежутке от 2 до 10 000.
Совершенными называются числа, сумма делителей которых с учётом единицы, но без учёта их самих равна самому числу. Пример: 6: 1 + 2 + 3 = 6. Соответственно недостаточными числами называются те сумма, указанных делителей которых, меньше самого числа. Пример: 10: 1 + 2 + 5 = 8. А в избыточных числах суммы указанных делителей больше самих чисел. Пример: 12: 1 + 2 + 3 + 4 + 6 = 16.
Для решения задачи мы будем просматривать все числа на промежутке от 2 до n и проверять, являются они совершенными, недостаточными или избыточными. Чтобы узнать каким является число, будем вычислять сумму его делителей и сравнивать её с самим числом. То есть, нам нужно для каждого числа вычислить сумму чисел, на которые оно делится без остатка. Так как значение самого числа при расчёте суммы делителей мы не учитываем, то наибольший возможный его делитель может быть равен только самому числу, делённому на 2. То есть при поиске делителей числа мы будем проверять все числа на промежутке от 1 до самого числа делённого на 2.
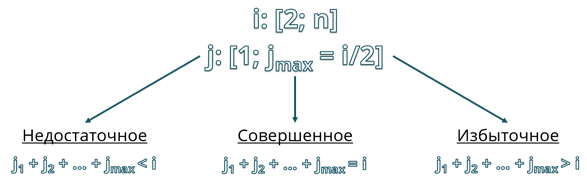
Составим блок-схему алгоритма решения задачи. В начале программа будет принимать на ввод число n. Нам понадобятся переменные для хранения количества совершенных, недостаточных и избыточных чисел. Назовём их соответственно sov, ned и izb. Так как мы ещё не считали числа, присвоим им всем значение 0. После этого запишем цикл с параметром, который будет перебирать все числа на промежутке от 2 до n. Назовём параметр цикла i. В цикле мы будем высчитывать сумму делителей для данного числа, назовём переменную для её хранения s. Так как в начале цикла мы её ещё не рассчитывали, присвоим s значение 0. Дальше будет следовать ещё один цикл с параметром для поиска делителей числа. Назовём его параметр j и он будет изменятся на промежутке от 1 до i/2. В нём мы будем проверять, является ли j делителем i, то есть равен ли остаток от деления i на j 0. Если это условие выполняется, то увеличим значение суммы делителей – s на j. Так по окончании работы внутреннего цикла мы вычислим сумму делителей s для числа i.
Теперь нам нужно сравнить полученную сумму с самим числом. Сначала проверим, является ли число i совершенным, для этого запишем блок ветвления с условием s = i. Если это условие выполняется, то мы увеличим значение счётчика совершенных чисел – sov на 1. В противном случае, проверим является ли i недостаточным числом, для этого запишем блок ветвления с условием s < i. Если это условие выполняется, увеличим значение счётчика недостаточных чисел – ned на 1. В противном случае? так как наше число не совершенное и не недостаточное, значит оно избыточное. Соответственно мы увеличим счётчик избыточных чисел – izb на единицу. Таким образом по окончании работы цикла мы переберём все числа от 2 до n и определим какие они. В конце программы нам остаётся лишь вывести на экран значения счётчиков: sov, ned и izb.
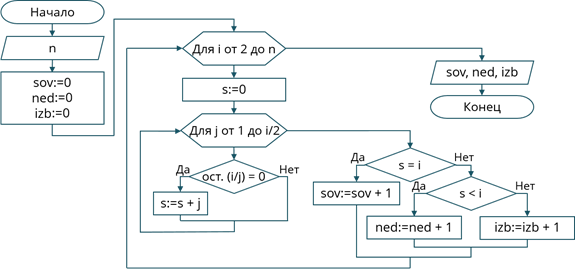
Блок-схема алгоритма решения задачи
Напишем программу по составленной блок-схеме. Назовём её chisla. Для работы программы нам потребуется переменные: n, i, j, s, sov, ned и izb. Так как n находится на промежутке от 2 до 10 000, а все остальные числа могут принимать значение не большее n, они все будут принадлежать к целочисленному типу integer.
Напишем логические скобки. Тело программы будет начинаться с оператора writeln, который выводит на экран сообщение о том, это программа подсчёта количества совершенных, недостаточных и избыточных чисел на промежутке от 2 до n. Дальше будет следовать оператор write, который будет выводить на экран запрос на ввод n и оператор readln, считывающий его значение. Теперь присвоим переменным sov, izb и ned значение 0. Дальше запишем цикл for i:=2 to n do для перебора всех чисел на промежутке, введённом пользователем. Так как он будет содержать больше одного оператора, запишем логические скобки. Тело цикла будет начинаться с присваивания s:=0. Теперь запишем вложенный цикл for j:=1 to i div 2 do, для расчёта суммы делителей i. В нём будет следовать один условный оператор с условием: i mod j = 0. После слова then в нём будет следовать оператор присваивания s:=s+j. После того, как мы рассчитали сумму делителей сравним её с самим числом i. Запишем условный оператор с условием: s = i. После слова then в нём будет следовать оператор, увеличивающий значение переменной sob на 1. После слова else запишем ещё один условный оператор с условием: s < i. В нём после слова then будет оператор увеличивающий значение переменной ned на единицу. А после слова else – оператор, увеличивающий izb на 1. На этом внешний цикл завершит работу. После него запишем оператор write, выводящий на экран сообщение о том, что на промежутке от 2 до n, количество совершенных чисел равно значению переменной sov, недостаточных – переменной ned, а избыточных – переменной izb.
program chisla;
var
n, i, j, s, sov, ned, izb: integer;
begin
writeln ('Программа подсчёта количества совершенных, недостаточных и избыточных чисел на промежутке [2; n].');
write ('n=');
readln (n);
sov:=0;
ned:=0;
izb:=0;
for i:=2 to n do
begin
s:=0;
for j:=1 to i div 2 do
if i mod j = 0
then s:=s+j;
if s = i
then sov:=sov+1
else if s < i
then ned:=ned+1
else izb:=izb+1;
end;
write ('На промежутке [2; ', n, '] находятся ', sov, ' совершенных, ', ned, ' недостаточных и ', izb, ' избыточных чисел.');
end.
Программа для решения задачи
Запустим программу на выполнение и зададим n = 10. На промежутке от 2 до 10 действительно 1 совершенное число, 8 недостаточных и 0 избыточных.

Снова запустим программу и зададим n = 1000. На промежутке от 2 до 1000 действительно 3 совершенных числа, 750 недостаточных и 246 избыточных.

Программа работает правильно. Задача решена.
Противоположностью циклов с заданным числом повторений являются итерационные циклы. Их число повторений заранее неизвестно. При каждом их повторении происходит последовательное приближение вычислений и проверяется условие цикла. Цикл выполняется до тех пор, пока не будет выполнено его условие. Как ясно из описания, итерационный цикл может быть реализован в программе только с помощью циклов с предусловием и постусловием.
Задача: Найти сумму элементов бесконечной последовательности с точностью e, заданной пользователем.


Как видим из формулы i-того элемента последовательности, при увеличении i будет увеличиватся знаминатель дроби, а значит значение самого элемента уменьшается. Так мы будем расчитывать значение суммы, пока очередной элемент последовательности не станет меньше введённого e. Также значение знаминателя дроби можно получить из предыдущего, увеличив его на i. Поэтому можно для экономии времени хранить знаминатель дроби и изменять его для i-того элемента.
Составим блок-схему алгоритма решения задачи. Сначала пользователь вводит с клавиатуры значение e. Сумму элементов последовательности мы будем хранить в переменной s. Присвоим ей значение 0, так как мы не расчитали ещё ни одного элемента последовательности. По этой же причине присвоим ноль переменной, которая будет хранить значение знаминателя дроби, назовём её z, а так же номеру текущего элемента – i. Теперь увеличим номер элемента последовательности на 1 и вычислим его. Для этого увеличим знаминатель дроби - z на i. После чего увеличим значение суммы элементов – s на значение текущего элемента последовательности, то есть на 1/z. Теперь проверим, меньше ли текущий элемент последовательности, чем e. Если это условие не выполняется, то мы вычислим следующий элемент последовательности и прибавим его к сумме – s, то есть мы вернёмся к оператору, увеличивающему значение i на 1. Если же условие выполняется – нам остаётся лишь вывести значение s на экран и на этом наш алгоритм завершит свою работу.

Блок-схема алгоритма решения задачи
Напишем программу по составленной блок-схеме. Назовём её summa. Для работы программы нам понадобится переменные: s и e, по условию задачи это будут действительные числа, поэтому объявим их вещественного типа real. Также нам понядобятся переменные: i и z. Эти переменные по условию будут целочисленного типа integer.
Напишем логические скобки. Тело программы будет начинаться с оператора writeln, выводящего на экран сообщение о том, что это программа расчёта суммы элементов последовательности с точностью e. Дальше будет следовать оператор write, выводящий на экран запрос на ввод e и оператор readln, считывающий его значение. Теперь запишем операторы присваивания переменным s, z, а также i значения 0. Теперь запишем оператор цикла с постусловием repeat. Сразу же запишем слово until с условием завершения работы цикла: 1/z < e. Тело цикла будет начинаться с оператора, увеличивающего значение i на 1. После чего мы увеличиваем на i значение z. А также значение s – на i-тый элемент последовательности, то есть на 1/z. После цикла запишем оператор write, выводящий на экран сообщение о том, что сумма элементов последовательности равна значению переменной s. Укажем формат вывода s, сделаем так чтобы выводилось 3 знака после запятой.
program summa;
var
s, e: real;
i, z: integer;
begin
writeln ('Программа расчёта суммы элементов последовательности с точностью е.');
write ('e=');
readln (e);
s:=0;
z:=0;
i:=0;
repeat
i:=i+1;
z:=z+i;
s:=s+1/z;
until 1/z < e;
write ('Сумма элементов последовательности равна ', s:0:3);
end.
Программа решения задачи
Аналитически можно доказать, что вычисляемая сумма стремится к 2. Запустим программу на выполнение и зададим e = 0,001. При e = 0,001, сумма действительно равна 1,957.

Снова запустим программу на выполнение и зададим e = 0,000001. Сумма при этой точности действительно равна 1,999.

Если мы ещё увеличим точность, к примеру, до e = 0,000000001, то при округлении до третьего знака после запятой сумма будет равна 2.

Программа работает правильно. Задача решена.
Важно запомнить:
· Вложенными называются циклы, которые выполняются внутри других циклов.
· Итерационным называется цикл, количество повторений которого заранее не известно. При каждом его повторении происходит последовательное приближение вычислений. В программах такие циклы реализуются с помощью циклов с пред и постусловием.

 Получите свидетельство
Получите свидетельство Вход
Вход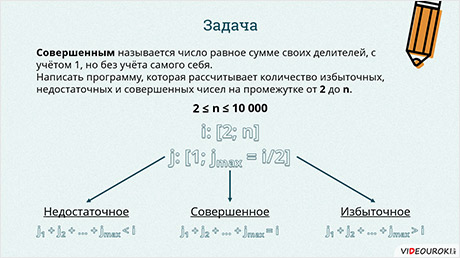




 4761
4761