Случайные события. Вероятность случайного события

Представим себе такую историю…

Саша и Паша встретились по дороге в школу, и между ними завязался такой разговор.

– Вероятно, меня сегодня вызовут к доске на уроке математики, – сказал Саша.

– Вполне вероятно, что и меня тоже сегодня вызовут к доске на уроке математики, – продолжил Паша.

– Тебя недавно спрашивали, – возразил Саша, – а меня давно не спрашивали. Значит, маловероятно, что тебя вызовут к доске сегодня, а вот меня вызовут с большей вероятностью.

– Согласен, – произнёс Паша, – но вероятность всё же есть, что меня тоже могут вызвать к доске.

– А давай спросим у Мудряша, кого же из нас скорее всего вызовут к доске, – предложил Саша.

– Давай – согласился Паша.

– Ребята, прежде чем я отвечу на ваш вопрос, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.

– Давайте сверимся! – сказал Мудряш. — Посмотрите, что у вас должно было получиться!

– Ну а теперь вернёмся к вашему вопросу, – начал Мудряш. – В вашем разговоре прозвучали такие слова, как «вероятно», «вполне вероятно», «маловероятно», «с большей вероятностью». Все эти слова связаны со словом «вероятность». Давайте разберёмся, что же такое вероятность.

– Итак, – продолжил Мудряш, – многое в нашей жизни, несмотря на то, что мы планируем заранее, зависит от случая. Купив лотерейный билет, мы можем выиграть, а можем не выиграть. Сегодня на уроке математики учитель может вызвать вас к доске, а может и не вызвать. Снег может выпасть, а может и не выпасть, чёрный кот может перебежать дорогу перед вами, а может и передумать. Всё это события. И каждое из этих событий в одних и тех же условиях могло произойти, а могло и не произойти.

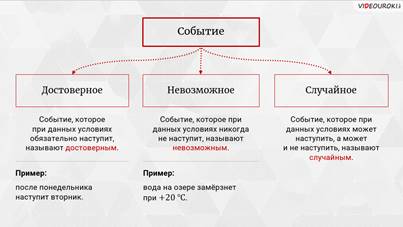
Запомните! Событие, которое при данных условиях может наступить, а может и не наступить, называют случайным.

– Разве в нашей жизни всегда происходят только случайные события? – спросил Паша.

– Вообще, событие бывает трёх видов: достоверное, невозможное и случайное, – продолжил Мудряш. – Событие, которое при данных условиях обязательно наступит, называют достоверным. Например, вы знаете, что после понедельника всегда наступает вторник. Это достоверное событие. Событие, которое при данных условиях никогда не наступит, называют невозможным. Например, вода на озере замёрзнет при + 20^о. Данное событие никогда не произойдёт при таком условии, значит, это событие невозможное.

А вы можете привести примеры достоверных и невозможных событий? – спросил у ребят Мудряш.

– Достоверными будут такие события: вода на озере замёрзнет при – 20^о, так как вода замерзает при минусовой температуре; дата рождения моего друга – число меньшее, чем 32, так как в каждом месяце не более 31 дня, – привёл примеры Паша.

– А невозможными будут такие события: среди ночи выглянуло солнце, при бросании игрального кубика выпадет 7 очков, – сказал Саша.

– Молодцы! – похвалил ребят Мудряш. – Но всё же в жизни всё не так чётко и ясно. Чаще всего мы сталкиваемся именно со случайными событиями, одни из которых более вероятны, другие — менее вероятны.

– А эти случайные события нельзя заранее предугадать? – спросил Паша.

– Хороший вопрос! – сказал Мудряш. – Очень часто нам важно знать, на сколько или во сколько раз одно случайное событие вероятнее другого. Существует специальная наука, которая занимается оценками вероятностей случайных событий. Называется эта наука теорией вероятностей.

Итак, вероятность наступления достоверного события можно охарактеризовать как стопроцентную, а вероятность наступления невозможного события — как нулевую. Так как 100 % – это  величины (в свою очередь, ), то договорились о следующем: вероятность достоверного события считается равной 1, вероятность невозможного события считается равной 0. Тогда вероятность случайного события может быть любым числом от 0 до 1.

– Давайте проведём небольшой эксперимент, – предложил Мудряш. – Будем подбрасывать монету, например рубль. Скажите, в результате этого эксперимента какие события могут произойти?

– Монета может упасть решкой вверх, – предположил Саша.

– Или монета может упасть орлом вверх, – сказал Паша.

– Правильно! – согласился Мудряш. – Случай «монета встала на ребро» считаем невероятным и не учитываем. Эксперимент с монетой – это достоверное событие: монета обязательно упадёт орлом или решкой вверх, третьего варианта не дано. Но оба исхода – выпадение орла или выпадение решки – равновозможны, или ещё можно сказать равновероятны. В результате эксперимента может произойти как первое событие, так и второе. Тогда вероятность каждого из этих событий будет равна отношению числа благоприятных случаев к числу равновозможных случаев.

Допустим, нас интересует исход выпадение орла – это благоприятный для нас случай. Тогда вероятность этого события будет равна отношению благоприятных случаев (таких случаев – 1) к числу всех равновозможных случаев (их 2), то есть равна . То же самое мы можем сказать и о вероятности события выпадение решки. Она тоже равна .

– Давайте проведём ещё один эксперимент, – предложил Мудряш. – Будем подбрасывать игральный кубик. Скажите, какие события могут произойти в результате этого эксперимента?

– В результате эксперимента с игральным кубиком можно получить один из 6 исходов: выпадет 1, 2, 3, 4, 5 или 6 очков, – сказал Паша.

– Хорошо! – согласился Мудряш. – Все эти 6 исходов равновозможны, и один из них обязательно произойдёт. Если нас интересует событие, например выпадение 2 очков, то вероятность данного события будет равна .

– А теперь представьте, что нас интересуют следующие события: первое — выпадение чётного числа очков; второе — выпадение числа очков, кратного числу 3. Определите вероятность этих событий.

– Событию выпадение чётного числа очков благоприятствуют 3 случая: выпадение 2, 4 или 6 очков, – начал Саша. – Тогда вероятность этого события равна отношению числа случаев, благоприятствующих этому событию (их 3), к числу всех равновозможных случаев (их 6). Значит, вероятность выпадения чётного числа очков равна  или .

– Событию выпадение числа очков, кратного числу 3, благоприятствуют только 2 случая: выпадение 3 или 6 очков, – сказал Паша. – Тогда вероятность этого события равна отношению числа случаев, благоприятствующих этому событию (их 2), к числу всех равновозможных случаев (их 6). Следовательно, вероятность выпадения числа очков, кратного числу 3, равна  или .

– Молодцы! – похвалил ребят Мудряш. – Приведённые примеры иллюстрируют следующее. Если эксперимент заканчивается одним из  равновозможных исходов, из которых  являются благоприятными для наступления данного события, то вероятность этого события равна .

– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.

Задание первое: в коробке лежит 3 красных и 7 синих шаров. Наугад вынимают 1 шар. Какова вероятность того, что этот шар окажется: красным; синим?

Решение: представим себе, что шары пронумерованы числами от 1 до 10, так как всего у нас 7 + 3 = 10 шаров в коробке. Тогда при вынимании шара может произойти 10 равновозможных исходов: вынули шар с номером один, вынули шар с номером 2 и так далее. В первом случае благоприятных исходов будет только 3 (ведь в коробке только 3 красных шара). Поэтому искомая вероятность равна .

Во втором случае благоприятных исходов будет 7, так как в коробке лежит 7 синих шаров. Поэтому искомая вероятность равна .

Задание второе: в коробке лежит 10 карточек, пронумерованных числами от 1 до 10. Какова вероятность того, что наугад будет вытянута карточка с чётным числом?

Решение: при вынимании карточек может произойти десять равновозможных исходов: вынули карточку с номером 1, вынули карточку с номером 2 и так далее. Но благоприятных исходов будет только 5: вынули карточку с номером 2, вынули карточку с номером 4, вынули карточку с номером 6, вынули карточку с номером 8 или вынули карточку с номером 10. Значит, искомая вероятность равна  или .