Объем конуса

Сегодня на уроке мы вспомним, какие фигуры мы назвали конусом, усечённым конусом, выведем формулы для вычисления объёма конуса и усечённого конуса.

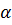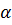Конус – это один из видов тел вращения. Рассмотрим произвольную плоскость , окружность  с центром , лежащую в плоскости  и прямую 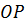, перпендикулярную к плоскости 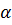 этой окружности. Через точку 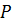 и каждую точку окружности проведём прямую.

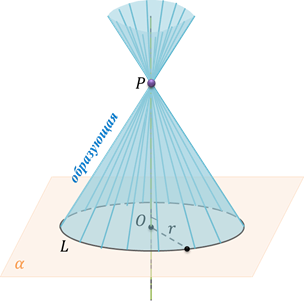
Определение:

Поверхность, образованная этими прямыми, называется конической поверхностью, а сами прямые – образующими конической поверхности.

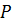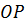Точка  называется вершиной, а прямая  называется осью конической поверхности.

Мы давали такое определение. Тело, ограниченное конической поверхностью и кругом с границей , называется конусом.

Вспомним элементы конуса.

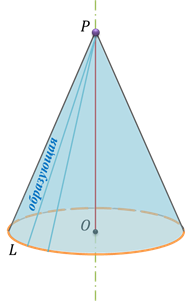
Основанием конуса называется круг, границей которого служит окружность .

Вершиной конуса называется вершина конической поверхности.

Образующими конуса называются отрезки образующих конической поверхности, заключённые между его вершиной и основанием. Отметим, что все образующие конуса равны друг другу.

Боковой поверхностью конуса называется фигура, образованная всеми образующими конуса.

Ось конической поверхности называется осью конуса. А её отрезок (или его длина), заключённый между вершиной и основанием, - высотой конуса.

Конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов на .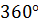

На экране изображён конус, полученный вращением прямоугольного треугольника 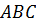 вокруг катета 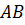. В этом случае основание конуса образуется вращением катета 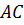, а боковая поверхность конуса – вращением гипотенузы .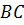

Теперь давайте сформулируем и докажем теорему.

Объём конуса равен одной трети произведения площади основания на высоту.

Доказательство. Рассмотрим конус с объёмом 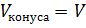, радиусом основания 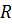, высотой  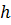и вершиной в точке .

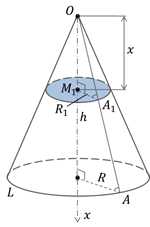
Проведём ось 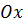 так, чтобы она проходила черев высоту конуса. Любое сечение конуса плоскостью перпендикулярной к оси 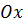 является кругом с центром в точке пересечения этой плоскости с осью 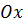. Например, с центром в точке 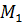. Обозначим радиус этого круга за 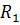, а площадь сечения обозначим за , где икс – абсцисса точки .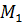

Поскольку ось 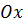 проходит через высоту конуса, то, значит, что ось 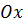 перпендикулярна плоскости основания, тогда плоскость сечения параллельна плоскости основания, значит, можно записать, что 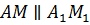. Из параллельности этих отрезков следует равенство углов 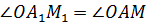, , 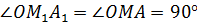отсюда следует подобие треугольников .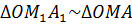

Из подобия можно записать равенство отношений 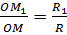. Отрезок 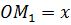,  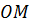– высота конуса, значит , тогда можно записать, что отношение .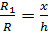

Отсюда нетрудно выразить 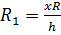. Площадь сечения равна 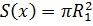. Подставим вместо  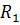его выражение через радиус основания конуса, получим, что .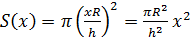

Для вычисления объёма воспользуемся основной формулой для вычисления объёмов тел.

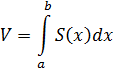
Пределы интегрирования от 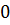 до 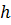, получим, что объём равен .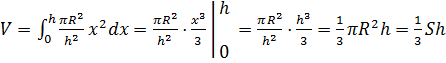

Что и требовалось доказать.

Следствием этой теоремы будет формула для вычисления объёма усеченного конуса. Но прежде чем сформулировать следствие, давайте вспомним, какую фигуру мы назвали усечённым конусом.

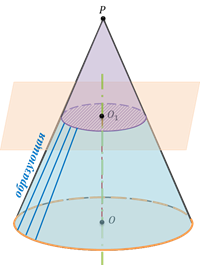
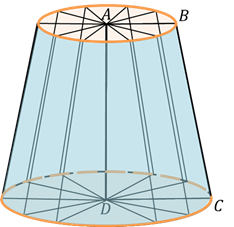
Усечённым конусом называется часть конуса, расположенная между его основанием и секущей плоскостью, перпендикулярной оси конуса.

Назовём элементы усечённого конуса.

Основание исходного конуса и круг, полученный в сечении этого конуса плоскостью, называются основаниями усечённого конуса.

Высотой усечённого конуса называется отрезок (или его длина), соединяющий центры его оснований.

Прямая 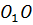 называется его осью.

Часть конической поверхности, ограничивающая усечённый конус, называется его боковой поверхностью, а отрезки образующих конической поверхности, расположенные между основаниями, называются образующими усечённого конуса.

Все образующие усечённого конуса равны друг другу.

Усечённый конус может быть получен вращением на 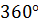 прямоугольной трапеции вокруг ее боковой стороны, перпендикулярной к основаниям.

Теперь сформулируем следствие.

Объём усечённого конуса, высота которой равна 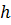, а площадь оснований равны 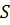 и 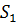, вычисляется по формуле:

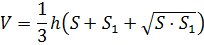
Решим несколько задач.

Задача: заполнить таблицу недостающими данными.

Решение: в первой строке нам известны радиус основания конуса и высота конуса, для того, чтобы найти объём конуса, воспользуемся только что доказанной формулой .

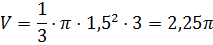
Занесём получившееся значение в ячейку.

Во второй строке нам даны объем конуса и радиус его основания, для того чтобы найти высоту конуса, выразим из формулы объёма высоту и получим 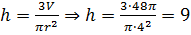. Занесём получившееся значение в ячейку.

В третьей строке нам даны: объём конуса и его высота нам необходимо найти радиус основания конуса. Подставим эти значения в известную нам формулу, выразим из неё высоту конуса и получим .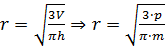

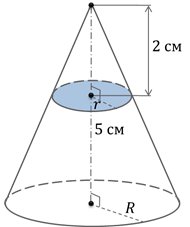
Задача: высота конуса равна 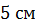. На расстоянии  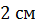от вершины его пересекает плоскость, параллельная основанию. Найти объём исходного конуса, если объём меньшего конуса, отсекаемого от исходного, равен .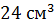

Решение: так как плоскость пересекает конус на расстоянии 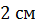 от вершины, значит, высота меньшего конуса равна 2 см.

Тогда зная объём меньшего конуса нетрудно найти радиус основания меньшего конуса .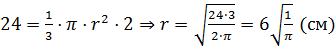

Большой конус и маленький конус подобны, поэтому можно записать равенства отношений .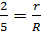

Отсюда нетрудно найти, что радиус основания большого конуса равен .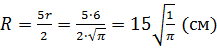

Тогда, подставив найденные значения в формулу для вычисления объёма, получим, что объём конуса равен .

Задача: радиусы оснований усечённого конуса равны 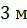 и 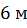, а образующая конуса равна 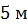. Найти объём усечённого конуса.

Решение: построим осевое сечение усечённого конуса.

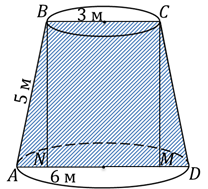
В осевом сечении будет равнобедренная трапеция, основаниями которой будут диаметры оснований конуса, а боковыми сторонами будут образующие усечённого конуса.

Опустим высоты трапеции, эти высоты будут равны высоте конуса. Поскольку трапеция равнобедренная, значит,  высоты разбивают трапецию на два равных прямоугольных треугольника и прямоугольник.

Нетрудно найти, что высота трапеции, а значит и усеченного конуса будет равна:

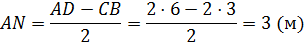
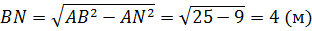
Вычислим площади оснований усечённого конуса.

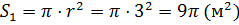
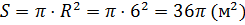
Подставим найденные значения в формулу для вычисления объёма усеченного конуса и получим, что объём усечённого конуса равен .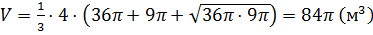

Итоги:

Сегодня на уроке мы вспомнили, какие фигуры называются конусом и усечённым конусом, вывели формулы для вычисления объёмов конуса и усечённого конуса. Решили насколько задач.