Объем пирамиды

Сегодня на уроке мы вспомним, какую фигуру мы назвали пирамидой, основные элементы пирамиды, выведем формулу для вычисления объёма пирамиды.

Давайте начнём с того, что вспомним, какую фигуру мы назвали пирамидой.

Определение:

Итак, рассмотрим многоугольник  и точку , не лежащую в плоскости этого многоугольника. Соединим точку  отрезками с вершинами многоугольника. В итоге получим  треугольников: , , … , . Многогранник, составленный из  -угольника  и этих  треугольников, называется пирамидой.

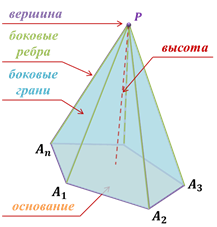
Многоугольник  называется основанием пирамиды.

Треугольники , , … ,  называются боковыми гранями пирамиды.

Точка  – вершиной пирамиды, а отрезки , , … ,  – её боковыми рёбрами.

Пирамиду с вершиной  и основанием  называют  -угольной пирамидой и обозначают так: .

Отрезок, соединяющий вершину пирамиды с плоскостью её основания и перпендикулярный к этой плоскости, называется высотой пирамиды.

Теперь давайте сформулируем и докажем теорему.

Объём пирамиды равен одной трети произведения площади основания на высоту.

Доказательство. Сначала давайте докажем теорему для треугольной пирамиды.

Рассмотрим треугольную пирамиду  с объёмом , площадью основания  и высотой .

Давайте проведём координатную ось  так, чтобы она проходила через высоту пирамиды.

Рассмотрим сечение  плоскостью, перпендикулярной к оси  и, значит, параллельной плоскости основания.

Обозначим через точку  точку пересечения плоскости  с осью , через  обозначим площадь сечения.

Выразим площадь сечения  через площадь основания пирамиды  и высоту пирамиды .

По рисунку нетрудно увидеть, что . Это действительно так. Это подобие вытекает из того факта, что сечение параллельно плоскости основания.

Раз треугольники подобны, значит, отношения .

Рассмотрим прямоугольные треугольники  и . Так как сечение , значит, отрезки , отсюда, углы  как соответственные углы. Значит, треугольники . Поэтому отношения . Длина отрезка , то есть отношения равны.

Поскольку в обоих равенствах присутствует отношение , то можно записать, что

То есть мы получили, что коэффициент подобия для треугольников
 и  равен . Тогда площади этих треугольников относятся .

Теперь давайте применим основную формулу для вычисления объёмов тел.

Границами интегрирования будут числа 0 и .

Получим, что объём равен .

Теперь давайте докажем эту теорему для произвольной пирамиды с высотой  и площадью основания . Такую пирамиду можно разбить на треугольные пирамиды с общей высотой , например, пятиугольную пирамиду можно разбить так.

Выразим объём каждой треугольной пирамиды по доказанной формуле.

Мы знаем, что если тело составлено из нескольких тел, то его объём равен сумме объёмов этих тел. Значит, объём пятиугольной пирамиды будет равен сумме объёмов треугольных пирамид.

Вынесем за скобку , в скобках получим сумму площадей оснований треугольных пирамид, а это есть ничто иное как площадь основания пятиугольной пирамиды.

Таким образом, объём произвольной пирамиды равен . Что и требовалось доказать.

Следствием из этой теоремы будет формула для вычисления объёма усечённой пирамиды.

Прежде чем сформулировать это следствие, давайте вспомним, какую пирамиду мы называем усечённой.

Пусть нам дана пирамида . Проведём секущую плоскость , параллельную плоскости основания пирамиды и пусть эта плоскость пересекает боковые рёбра в точках , , …, . Плоскость  разбивает пирамиду на две фигуры: пирамиду  и многогранник.

Определение:

Многогранник, гранями которого являются   и , расположенные в параллельных плоскостях и  четырехугольников ,  и так далее  называется усечённой пирамидой.

 -угольники  и  называются соответственно верхним и нижним основанием.

Четырёхугольники ,  и так далее  называются боковыми гранями.

,  и так далее  называются боковыми рёбрами усечённой пирамиды.

Усечённую пирамиду обозначают так .

Возьмём на верхнем основании произвольную точку  и из этой точки опустим перпендикуляр на нижнее основание. Этот перпендикуляр называется высотой усечённой пирамиды.

Объём усечённой пирамиды, высота которой равна , а площадь оснований равны  и , вычисляется по формуле:

Решим несколько задач.

Задача: найти объём правильной треугольной пирамиды, высота которой равна , а сторона основания равна .

Решение: поскольку пирамида правильная, значит, в основании лежит правильный, то есть равносторонний треугольник.

Площадь равностороннего треугольника со стороной 13 см равна .

Применим формулу для вычисления объёма, подставим числа, выполним элементарные преобразования и получим, что объём призмы равен .

Задача: в правильной усечённой четырёхугольной пирамиде стороны основания равны  и , а площадь сечения пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани, равна . Найти объём усеченной пирамиды.

Решение: воспользуемся формулой для вычисления объёма усечённой пирамиды.

Площадь оснований этой пирамиды найти нетрудно, эти площади равны  и .

Рассмотрим сечение пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани. Этим сечением будет трапеция, причем высота этой трапеции будет высотой усечённой пирамиды, потому что высотой усечённой пирамиды называется перпендикуляр, опущенный на нижнее основание.

Высоту мы найдём пользуясь формулой для вычисления площади трапеции.

Основания трапеции – диагонали квадратов, то есть основания трапеции соответственно равны  и . Получим, что высота трапеции равна .

Подставив найденные значения в формулу для вычисления объёма усечённой пирамиды, мы получим, что объём усечённой пирамиды равен .

Итоги:

Сегодня на уроке мы вспомнили такие фигуры как пирамида, усечённая пирамида, вывели формулы для вычисления объёма пирамиды, усечённой пирамиды. Решили несколько задач.