Объем шара

На этом уроке мы дадим определение шара. Выведем формулу для вычисления объёма шара. А затем с её помощью выведем формулу для вычисления площади сферы.

Прежде чем приступить к рассмотрению данной темы, давайте вспомним, что такое шар.

Определение:

Шар – это совокупность всех точек пространства, находящихся от данной точки на расстоянии, не больше данного. Причём, данная точка называется центром шара, а данное расстояние – радиусом шара.

Радиусом шара называют всякий отрезок, соединяющий центр шара с любой точкой шаровой поверхности.

Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром шара. Диаметр шара равен двум радиусам.

Отрезок, соединяющий две точки шаровой поверхности и не являющийся диаметром шара, т.е. не проходящий через центр шара, называется хордой шара.

Понятно, что сечение шара плоскостью есть круг.

Сечение шара плоскостью, проходящей через его центр, называется большим кругом шара.

Итак, справедлива следующая теорема: объём шара радиуса  равен .

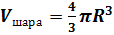Докажем теорему. Пусть нам дан шар радиуса  с центром в точке 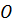. Выберем ось 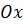 так, чтобы начало оси совпадало с центром шара.

Тогда отрезок  это есть радиус шара .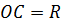

Докажем, что объём шара равен .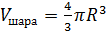

На оси 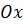 отметим произвольную точку 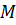 и рассмотрим сечение шара плоскостью проходящее через эту точку перпендикулярно к оси 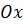. Заметим, что такое сечение шара плоскостью является кругом с центром в точке .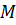

Отрезок .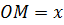

Обозначим радиус этого круга через , а его площадь через 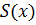, где 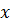 – абсцисса точки .

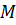Выразим площадь 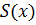 через 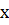 и радиус шара .

Из прямоугольного треугольника  по теореме Пифагора найдём радиус круга. Тогда имеем .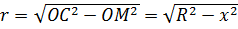

Площадь круга 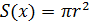. Заменим радиус круга  выражением . Тогда получаем, что .

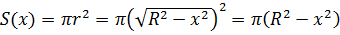Заметим, что эта формула верна для любого положения точки 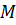 на диаметре 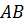. Иначе говоря, верна для всех 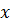, удовлетворяющих условию .

Так как мы с вами выразили площадь через 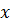, то можем вычислить объём шара с помощью основной формулы объёма тела. Вспомним её: объем тела равен .

Итак, применяя основную формулу для вычисления объёмов тел получаем, что объём шара равен .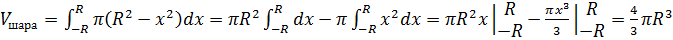

Этим мы с вами доказали, что объём шара с радиусом равным  можно вычислить по формуле .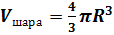

Что и требовалось доказать.

Ранее мы с вами без доказательства привели формулу для вычисления площади сферы. Напомню, что площадь сферы можно вычислить по формуле: .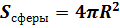

Теперь давайте выведем эту формулу, пользуясь формулой объёма шара.

Итак, рассмотрим сферу радиуса 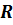 с центром в точке О и описанный около неё многогранник, имеющий 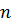 граней.

Напомним, что многогранник называется описанным около сферы (шара), если сфера касается всех его граней. При этом сфера называется вписанной в многогранник.

Занумеруем грани в произвольном порядке и обозначим через 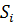 – площадь -й грани.

Затем соединим центр О сферы отрезками со всеми вершинами многогранника. При этом получим эн пирамид с общей вершиной О, основаниями которых являются грани многогранника, а высотами – радиусы сферы, проведенные в точки касания граней многогранника со сферой.

Следовательно, объём -й пирамиды равен , а объём всего описанного многогранника равен: . Где 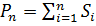 – площадь поверхности многогранника.

Отсюда получаем: .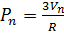

Теперь будем неограниченно увеличивать 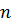 таким образом, чтобы наибольший размер каждой грани описанного многогранника стремился к нулю. При этом объём 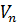 описанного многогранника будет стремиться к объёму шара. В самом деле, если наибольший размер каждой грани описанного многогранника не превосходит 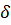, то описанный многогранник содержится в шаре радиуса 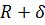 с центром в точке .

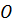Но ведь с другой стороны, описанный многогранник содержит исходный шар радиуса 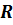. Значит, объём .

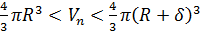Так как выражение  при 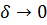, то и объем  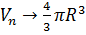при  ().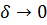

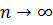Переходя затем к пределу, получаем, что .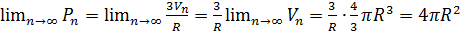

По определению площади сферы , следовательно, .  

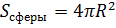Что и требовалось доказать.

Задача: объём шара равен равен  см³. Найдите диаметр шара.

Решение: запишем формулу для вычисления объёма шара.

По условию задачи объём шара равен  см³.

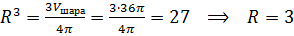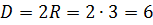Отсюда видим, что радиус шара равен  (см). Напомним, что диаметр шара вдвое больше его радиуса. Тогда диаметр нашего шара равен  (см).

Запишем ответ.

Задача: радиус шара увеличили в 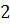 раза. Во сколько раз увеличился объём шара?

Решение: запишем формулу для вычисления объёма шара.

Так как по условию задачи радиус исходного шара увеличили в 2 раза, то радиус данного шара будет равен 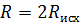. Подставляя данный радиус в формулу для вычисления объёма шара 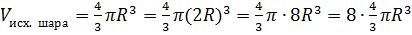 видим, что объём исходного шара увеличился в 8 раз. Следовательно, ответ: объём шара увеличился в 8 раз.

Задача: в цилиндр вписан шар. Найдите отношение объёма шара к объёму цилиндра.

Решение: шар, вписанный в цилиндр, касается оснований цилиндра в их центрах и боковой поверхности цилиндра по окружности большого круга, параллельной основаниям цилиндра. Отсюда следует, что 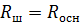, а высота цилиндра равна .

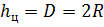Объём шара вычисляется по форму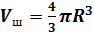ле , а объём данного цилиндра можно вычислить по формул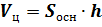е , где  – это площадь основания,  - высота цилиндра. Так как высота данного цилиндра равна двум радиусам, а площадь основания равна 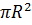, то объём цилиндра равен .

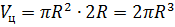Найдём отношение объёма шара к объёму цилиндра. Получаем, что объём шара относится к объёму цилиндра, как .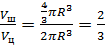

Эту задачу называют «Задачей Архимеда». Во времена Архимеда формула объёма шара была неизвестна. Поэтому данная задача считалась очень трудной и, решив ее, Архимед испытал большую радость. На могиле Архимеда был поставлен памятник с изображением шара и описанного около него цилиндра.

Итоги:

На этом уроке мы дали определение шара. Вывели формулу для вычисления объёма шара. А затем с её помощью вывели формулу для вычисления площади сферы.