Хорошо, когда, решая какую-нибудь задачу, вы можете видеть перед глазами всевозможные варианты решения. Например, вы хотите учиться в каком-то определённом городе N, в котором есть 2 высших учебных заведения, подготавливающих специалистов по 15-ти профессиям.

Значит, всего у вас есть пятнадцать вариантов выбора будущей профессии.
Теперь выбирать будет гораздо удобнее. Достаточно отбросить те профессии, которые по тем или иным причинам вам не подходят.
В 1942 году швейцарский учёный Фриц Цвикки предложил метод поиска решений технических задач, который был назван морфологическим или типологическим анализом.

Здесь «морфологический» имеет несколько другое значение, не то, о котором шла речь на уроках русского языка. В данном случае «морфологический» употребляется в значении «касающийся внешнего вида или строения». Другими словами, формы. Именно благодаря этому методу, учёному за довольно короткое время удалось решить несколько сложных задач в ракетостроении, которые ставили в тупик других специалистов.
Разберём суть этого метода. Сначала выделяются морфологические или, по-иному, отличительные признаки, которые значимы именно для конкретной решаемой задачи. А затем составляются всевозможные сочетания этих признаков.
Удобнее всего это делать в таблицах, которые назвали морфологическим ящиком или матрицей.
Рассмотрим этот метод на примере.
Перед выпускниками школы стоит острый вопрос о том, кем быть. Например, Паша хочет выбрать одну из трёх специальностей: учитель химии, врач или фармацевт.
Поможем ему определиться с помощью морфологической таблицы.

Так, как это понимает Паша.
Подсчитав общее количество баллов, нетрудно понять, что для Паши будет лучше выбрать профессию врача. Но для кого-то другого, например, подруги Паши – Оли, выбор профессии по таким же параметрам покажет, что оптимальный вариант для неё – стать фармацевтом.

Другими словами, такой способ выбора решения задачи подходит для всех потому, что каждый для себя может составить список важных параметров, составить шкалу и расставить баллы.
Применять такой метод можно для составления списка возможных вариантов решения задачи, для сравнения или выбора одного из многих решений как технических, так и организационных задач.
Но у этого метода есть один весомый недостаток. Это наличие большого количества вариантов, среди которых трудно выбрать оптимальный. Кроме того, очень трудно понять, все ли варианты рассмотрены.
Но бывают случаи, когда одномерная матрица нам не подходит. Например, мы решили сделать необычную визитку. С содержанием визитки проблем нет, но вот во внешнем оформлении хотелось бы чего-нибудь необычного.
Составим таблицу.

Подсчитать всевозможные варианты нетрудно. Достаточно количество вариантов материала (в нашем случае их 7) перемножить с количеством вариантов формы (в нашем случае их 4). Получится 28 вариантов.
Теперь остаётся рассмотреть все полученные варианты и исключить те из них, которые изготовить не представляется возможным, а также те, которые делают стоимость визиток заоблачной. Например, визитка, изготовленная из стекла, будет достаточно хрупкой и пользоваться ею будет неудобно, а изготовление металлической визитки – довольно затратное производство и так далее.
После анализа полученных вариантов, мы отбросим ненужные и получим оптимальную для нас визитку. Ещё раз обратите внимание на то, что в данном случае визитка будет оптимальной именно для нас, а другие могут отбросить выбранный нами вариант по причине того, что он дорогой или, например, сложный в исполнении.
Но могут возникнуть задачи, для которых двухмерной матрицы будет мало.
Рассмотрим такой пример.
Представьте себе, что перед вами стоит задача разработать упаковку для молока. Давайте попробуем составить морфологический ящик.
Для создания упаковки нам необходимо определить несколько параметров. Во-первых, решить, каковыми будут материал упаковки, её форма, укупорка, то есть, как эта упаковка будет закрываться, необходимо предусмотреть время использования и, что немаловажно, как эта упаковка будет утилизироваться.
Теперь давайте запишем всевозможные варианты.

Теперь мы можем составить множество различных вариантов. Вот один их них: упаковка в виде стеклянного цилиндра с одноразовой пробкой, многоразовая, которую для утилизации надо сдавать в пункт приёма. Этот вариант нам хорошо знаком – обыкновенная стеклянная бутылка молока с пробкой из фольги. Но кроме всех известных вариантов, при комбинации можно получить совсем неожиданные. Например, деревянная бутылка необычной формы без пробки, многоразовая, которую надо утилизировать в специальном пункте. Общее количество вариантов посчитать нетрудно. Достаточно перемножить количество вариантов в каждом из признаков.
Таким образом, мы получим 480 всевозможных вариантов. Останется только отбросить варианты, которые нам не подходят. Например, молоко хорошо хранится в сосуде из можжевельника, но производство такой тары достаточно затратно, а цена на конечный продукт станет неконкурентоспособной, поэтому все варианты с этим видом материала лучше отбросить. В итоге останутся варианты, которые и помогут найти верное решение.
Ещё раз хотелось бы обратить ваше внимание на то, что оптимальным и приемлемым решение будет в конкретном случае и для конкретных людей.
Для других оптимальным решением может быть абсолютно другое.
Подведём итоги урока.
Сегодня мы поговорили о таком методе выбора оптимального решения, как морфологический анализ.
Познакомились с сутью этого метода, сферами его применения и недостатками. Рассмотрели примеры выбора решения с помощью одномерных, двумерных и многомерных морфологических матриц.

 Получите свидетельство
Получите свидетельство Вход
Вход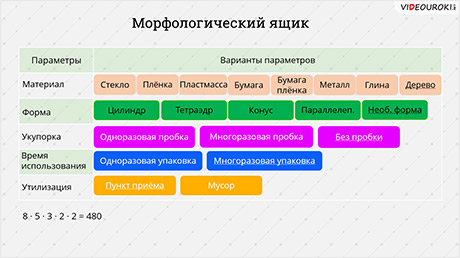



 0
0 5405
5405

