Прежде, чем приступить к рассмотрению новой темы,
вспомним,
что квадрат расстояния между точкой 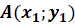 и
точкой
и
точкой 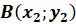 выражается
следующей формулой:
выражается
следующей формулой: 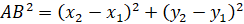 .
Вспомним основное тригонометрическое тождество:
.
Вспомним основное тригонометрическое тождество: 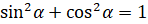 ,
а также формулы, выражающие зависимость
между синусами, косинусами, тангенсами и котангенсами противоположных углов:
,
а также формулы, выражающие зависимость
между синусами, косинусами, тангенсами и котангенсами противоположных углов:
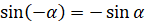 ,
, 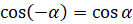 ,
, 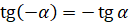 .
.
Теперь мы с вами познакомимся с формулами
сложения. Давайте докажем, что для любых углов 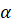 и
и 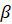 справедливо равенство:
справедливо равенство: 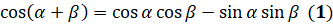 .
.
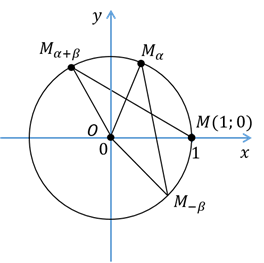
Доказательство. Пусть на координатной плоскости изображена единичная окружность
с центром в начале координат. Точка 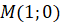 совершает поворот на угол
совершает поворот на угол 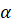 и оказывается в точке
и оказывается в точке 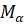 . Затем точка
. Затем точка 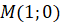 совершает поворот на угол
совершает поворот на угол 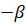 и оказывается в точке
и оказывается в точке 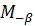 . И совершает поворот на угол
. И совершает поворот на угол 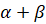 и оказывается в точке
и оказывается в точке 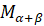 .
.
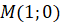 . По определению синуса и косинуса:
. По определению синуса и косинуса: 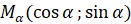 ),
), 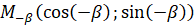 ,
,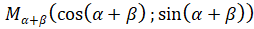 .
.
Давайте рассмотрим треугольники 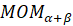 и
и 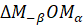 . Эти треугольники равнобедренные, так как две стороны каждого из
них являются радиусами нашей единичной окружности. При этом
. Эти треугольники равнобедренные, так как две стороны каждого из
них являются радиусами нашей единичной окружности. При этом 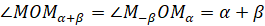 . Следовательно, рассматриваемые треугольники равны по двум
сторонам и углу между ними, то есть по первому признаку равенства треугольников.
А значит, основания этих равнобедренных треугольников равны, то
. Следовательно, рассматриваемые треугольники равны по двум
сторонам и углу между ними, то есть по первому признаку равенства треугольников.
А значит, основания этих равнобедренных треугольников равны, то 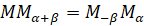 . Квадраты этих оснований также равны:
. Квадраты этих оснований также равны: 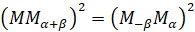 .
.
Применим к левой и правой частям последнего равенства формулу, выражающую квадрат расстояния между двумя
точками: 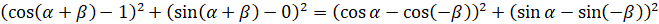 .
.
Преобразуем это выражение. В первую очередь воспользуемся
известными нам формулами и запишем в правой части 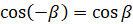 , а
, а 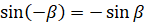 :
: 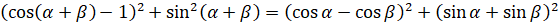 . Теперь воспользуемся формулой квадрата разности и выполним
возведение в квадрат в левой части, воспользуемся формулами квадрата разности и
квадрата суммы и выполним возведение в квадрат в правой части:
. Теперь воспользуемся формулой квадрата разности и выполним
возведение в квадрат в левой части, воспользуемся формулами квадрата разности и
квадрата суммы и выполним возведение в квадрат в правой части:
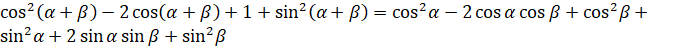 .
.
По основному тригонометрическому тождеству в левой части сумма
первого и последнего слагаемых равна 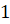 , в правой части
, в правой части 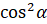 и
и 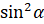 равна
равна 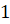 , а также сумма
, а также сумма 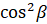 и
и 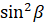 равна
равна 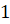 :
: 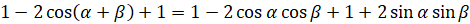 . Теперь выполним несложные преобразования:
. Теперь выполним несложные преобразования: 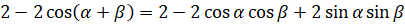 ,
, 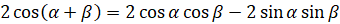 . И в результате получим, что
. И в результате получим, что 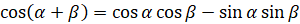 . Что и требовалось доказать.
. Что и требовалось доказать.
Теперь в доказанной формуле 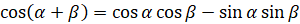 заменим
заменим 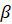 на
на 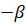 :
: 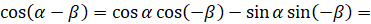 [воспользуемся известными нам формулами
[воспользуемся известными нам формулами 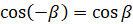 ,
, 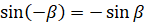 ]
] 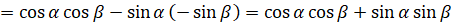 . Таким образом, получили
. Таким образом, получили 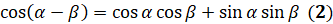 .
.
Мы познакомились с формулами сложения для косинуса. А для синуса
есть такие формулы? Прежде чем познакомиться с формулами сложения для синуса,
давайте докажем следующие формулы: 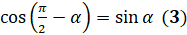 и
и 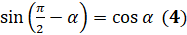 . Для этого в формулу
. Для этого в формулу 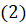 вместо
вместо 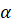 подставим
подставим  :
: 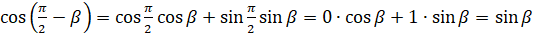 . Таким образом,
. Таким образом, 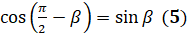 . Если мы заменим в этой формуле
. Если мы заменим в этой формуле 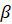 на
на 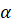 , то получим формулу
, то получим формулу 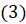 .
.
А если мы в формулу 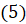 вместо
вместо 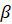 подставим
подставим 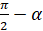 :
: 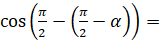
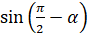 . Выполним преобразования:
. Выполним преобразования: 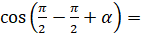
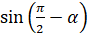 ,
, 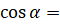
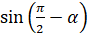 . И поменяем местами правую и
левую части, то получим формулу
. И поменяем местами правую и
левую части, то получим формулу 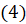 .
.
Далее, применяя все полученные выше формулы, мы с вами выведем
формулы сложения для синуса. Итак, применив формулу 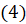 справа налево, запишем
справа налево, запишем 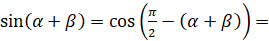 [перепишем выражение под знаком косинуса]
[перепишем выражение под знаком косинуса] 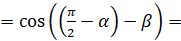 [применим формулу
[применим формулу 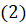 ]
] 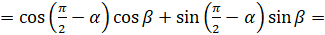 [по формуле
[по формуле 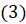 вместо к
вместо к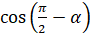 запишем
запишем 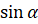 , по формуле
, по формуле 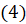 вместо
вместо 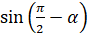 запишем
запишем 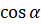 ]
] 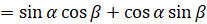 . Таким образом, мы получили, что
. Таким образом, мы получили, что 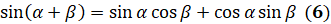 .
.
Теперь в формуле 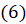 заменим
заменим 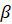 на
на 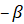 :
: 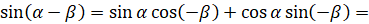 [в правой части
[в правой части 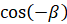 запишем как
запишем как 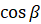 ,
, 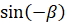 запишем как
запишем как 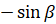 ]
] 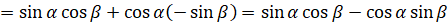 . Получаем:
. Получаем: 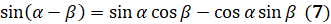 .
.
Таким образом, мы познакомились с формулами, которые называют формулами сложения.
Давайте вычислим 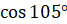 ,
, 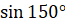 .
.
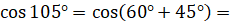 [применим формулу
[применим формулу 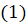 ]
] 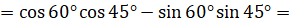 [подставим значения синусов и косинусов]
[подставим значения синусов и косинусов] 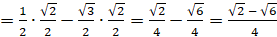 .
.
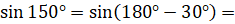 [применим формулу
[применим формулу 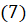 ]
] 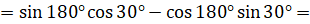 [теперь подставим значения синуса и косинуса]
[теперь подставим значения синуса и косинуса] 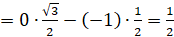 .
.
Сейчас, прежде чем приступить к практической части нашего урока,
давайте докажем следующее равенство: 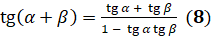 . Для этого запишем левую часть этого равенства как
. Для этого запишем левую часть этого равенства как 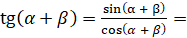 [преобразуем числитель по формуле
[преобразуем числитель по формуле 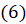 , а знаменатель преобразуем по формуле
, а знаменатель преобразуем по формуле 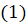 ]
] 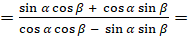 [теперь разделим числитель и знаменатель дроби на произведение
[теперь разделим числитель и знаменатель дроби на произведение 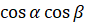 . При этом отметим, что
. При этом отметим, что 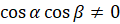 , так как делить на нуль нельзя]
, так как делить на нуль нельзя] 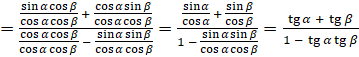 . Равенство
. Равенство 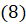 доказано.
доказано.
Это формула сложения для тангенса? Верно. Аналогичным образом
можно доказать, что 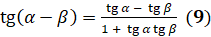 .
.
Давайте вычислим:
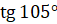 .
. 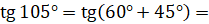 [применим формулу
[применим формулу 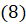 ]
] 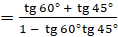 .
.
Подставим значения 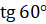 и
и 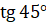 :
:
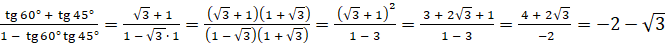 .
.
А сейчас выполним несколько заданий.
Задание первое. Вычислите: а) 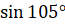 ; б)
; б) 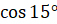 ; в)
; в) 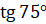 .
.
Решение.
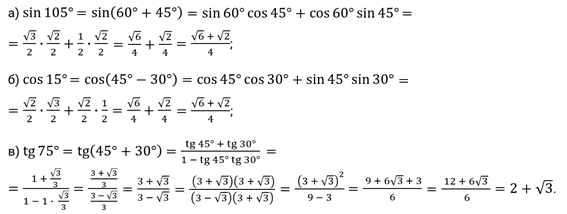
Второе задание. Найдите значения выражений: а) 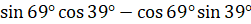 ; б)
; б) 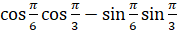 ; в)
; в) 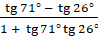 .
.
Решение.
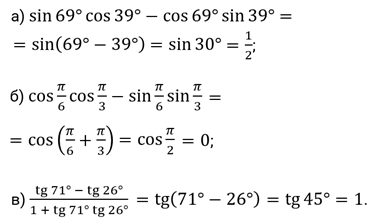

 Получите свидетельство
Получите свидетельство Вход
Вход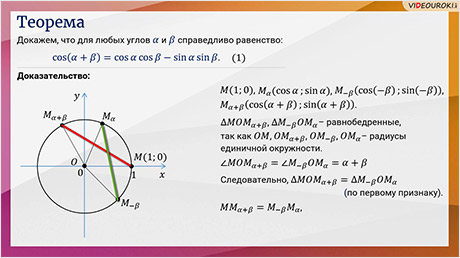



 0
0 5278
5278


