Деление и дроби

Сегодня мы продолжим изучать дроби.

Деление – как одну из операций в математике вы изучаете уже на протяжении нескольких лет в школе. До этого вы научились делить большее число на меньшее. А теперь давайте разберёмся можно ли делить наоборот – меньшее число на большее.

Рассмотрим пример из жизни. Наверняка вам приходилось делить что-то целое на несколько человек. Вот, например, у вас есть 2 шоколадки и их нужно разделить между 3 желающими её съесть. Как же это сделать?

Давайте разломаем каждую плитку шоколада на 3 части. В итоге у нас получилось 6 равных частей. Каждая из этих частей – это  часть шоколадки. Раздадим каждому по такой части от каждой шоколадки.

Видим, что каждый из детей получил по 2 такие части, т.е. . Вместе же это будет равно  плитки шоколада.

Мы с вами смогли разделить 2 целые шоколадки на 3-ёх детей!

Дробь  получилась в результате деления двух шоколадок на 3 равные части. Поэтому черту дроби можно понимать, как знак деления, т.е. .

Из этого примера хорошо видно, что знак деления и черта дроби – это одно и то же математическое действие. С помощью дробей можно записать результат деления двух любых натуральных чисел. Если деление выполняется нацело, то частное является натуральным числом.

Например

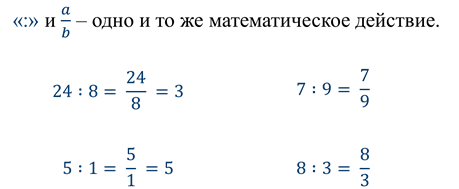
Любое натуральное число можно записать в виде дроби с любым натуральным знаменателем.

Например

Из этой записи видно, что числитель дроби равен произведению этого числа на знаменатель.

Решим уравнение:

Мы уже с вами знаем равенство сложения дробей с одинаковыми знаменателями:

Перепишем его справа налево.

С учётом того, что черта дроби есть то же самое, что и деление, то это равенство можно переписать так:

Получили ещё одно правило, которое стоит запомнить:

Если нужно разделить сумму чисел на число, то можно разделить каждое слагаемое на это число, а потом полученные частные сложить.

Пример

Итоги

Итак, сегодня на уроке мы с вами разобрались, как разделить меньшее число на большее, а также изучили ещё несколько свойств деления.