Данная тема посвящена разбору решений задач с использованием закона Архимеда и условий плавания тел.
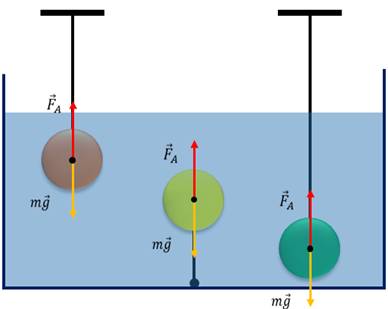
Задача 1. Три шарика одинаковых размеров погружены в воду и удерживаются нитями на разной глубине. Сравните выталкивающие силы, действующие на каждый шарик.
РЕШЕНИЕ
И так, как видно из рисунка, все три шарика полностью находятся под водой. Известно, что на любое тело, погруженное в жидкость или газ действует выталкивающая сила, которая, согласно закону Архимеда, равна весу жидкости в объеме погруженной части тела, направленная вертикально вверх и приложенная в центре давления.
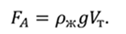
Эта сила пропорциональна объёму погружённой в жидкость части тела. Согласно условию задачи, все три шарики имеют одинаковый объём. Значит можно заключить, что на все шарики действует одинаковая выталкивающая сила.
ОТВЕТ: на все шарики действует одинаковая архимедова сила.
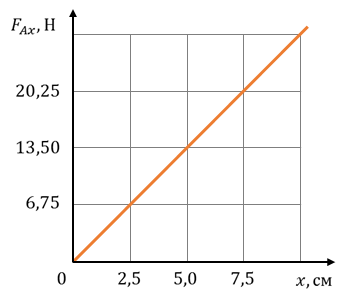
Задача 2. На графике показана зависимость модуля силы Архимеда, действующей на медленно погружаемый в жидкость кубик, от глубины погружения. Длина ребра кубика равна 10 см, его нижнее основание все время параллельно поверхности жидкости. Определите плотность жидкости.
РЕШЕНИЕ
На погружаемый в жидкость кубик действует выталкивающая сила, которая, согласно закону Архимеда, прямо пропорциональна плотности жидкости и объему погруженной части тела.

Задача 3. Тело плавает на границе раздела двух жидкостей с плотностями ρ1 и ρ2, погрузившись во вторую жидкость на 0,6 своего объема. Определите выталкивающую силу, действующую на тело, если ρ1 < ρ2.

Задача 4. Аэростат, объем шара которого 6000 м3, начинает равноускоренно подниматься вертикально вверх. Масса водорода, заполняющего шар, оболочки шара, команды и оборудования аэростата 500 кг. На какую высоту поднимется аэростат за 10 с движения, если плотность воздуха 0,15 кг/м3, а сопротивление воздуха пренебрежимо мало?


Задача 5. Какую работу необходимо совершить, чтобы плоскую льдину, толщина которой 0,2 м, полностью погрузить в воду, если площадь основания льдины равна 1,2 м2? Плотность льда и воды соответственно равны 900 и 1000 кг/м3.

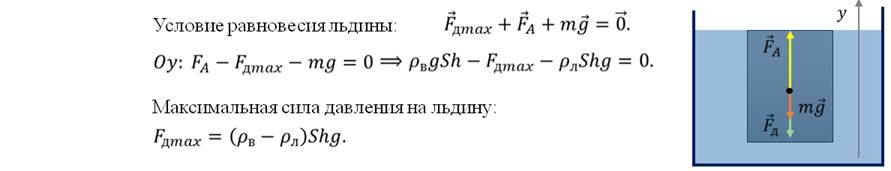
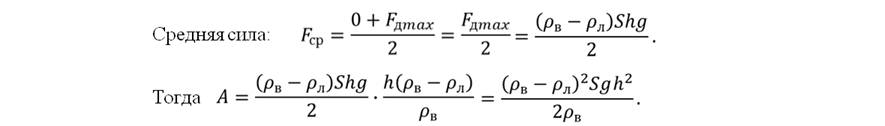

«Если вы хотите, чтобы другие верили в вас,
вы должны сначала убедить их, что верите в них»
Архимед

 Получите свидетельство
Получите свидетельство Вход
Вход




 0
0 7403
7403

