Здравствуйте, ребята!

Вы знаете, сегодня я услышал спор двух муравьёв, Касьяна и Демьяна, каждый из которых принёс в муравейник по пять гусениц и по восемь мух. И никак они не могут договориться, как же правильно сосчитать, сколько всего гусениц и мух они принесли в муравейник.
Касьян говорит, что надо сначала выяснить, сколько всего гусениц и мух принёс каждый из них, а потом узнать общее количество мух и гусениц, которое они принесли.
А Демьян утверждает, что надо сначала узнать, сколько всего гусениц, потом – сколько всего мух, а уж потом, сколько всего мух и гусениц принесли в муравейник.
Спорили они, спорили, да так ни до чего и не договорились. А ведь каждый из них по-своему был прав. Можно было узнавать таким способом, который предлагал Касьян.
Сначала узнать, сколько всего гусениц и мух принёс каждый муравей, а потом - сколько всего гусениц и мух принесли они вдвоём.

(5 + 8) ∙ 2 = 26 (г. и м.)
Ответ: всего 26 гусениц и мух муравьи принесли в муравейник.
А можно эту задачу решить и таким способом.

Сначала узнать, сколько гусениц принесли они вдвоём, потом – сколько мух они принесли, и затем, сколько всего гусениц и мух.
5 ∙ 2 + 8 ∙ 2 = 16 (г. и м.)
Ответ: всего 26 гусениц и мух муравьи принесли в муравейник.
Посмотрите, задача решена двумя способами.

Но в первом способе мы сначала нашли сумму чисел пять и восемь, а потом умножили её на два. А во втором способе мы числа пять и восемь по очереди умножали на два, а потом нашли сумму полученных чисел.
При решении этой задачи в каждом из способов были свои положительные и отрицательные стороны. Первый способ короче, но в нём есть умножение двузначного числа, а во втором способе можно использовать таблицу умножения, но, зато, этот способ – чуть длиннее.
Но, самое, главное, оказывается, можно умножить сумму на число, а можно – каждое слагаемое по очереди умножить на это число и полученные произведения сложить – результат от этого не изменится. Такое свойство умножения называется распределительным.
А теперь я предлагаю вам найти значение нескольких числовых выражений.
(4 + 2) ∙ 9
(7 + 8) ∙ 6
Посмотрите на первое из них. Как вы думаете, можно ли при его решении воспользоваться распределительным свойством умножения? Конечно можно. Ведь мы только что говорили, что можно умножить сумму на число (или число на сумму), а можно – каждое слагаемое по очереди умножить на это число и полученные произведения сложить – результат от этого не изменится.
А каким способом удобнее находить значение этого выражения? Попробуем оба способа. Сначала решим так, как оно записано. Сумма чисел четыре и два равна шести. Произведение чисел шесть и девять равно пятидесяти четырём. Ничего сложного, если уверенно знаешь таблицу умножения.
Попробуем воспользоваться распределительным свойством умножения. Найдём произведение чисел четыре и девять и произведение чисел два и девять, а потом сложим результаты. Здесь тридцать шесть, здесь – восемнадцать. Складываем числа гм-м-м. Тоже пятьдесят четыре. Пожалуй, этот способ здесь не очень удобен – он длиннее, и складывать числа тридцать шесть и восемнадцать не очень удобно. Лучше воспользоваться первым способом.
Решаем второй пример. Сумма чисел семь и восемь равна пятнадцати. И пятнадцать умножить на шесть. Упс, да это умножение нам ещё не по зубам. Надо попробовать применить распределительное свойство умножения.
Семью шесть плюс восемью шесть. Так, здесь сорок два, здесь сорок восемь, а всего… девяносто! Так вот в каких случаях распределительное свойство умножения будет просто палочкой-выручалочкой! Отлично! Действительно, это правило надо выучить!
Чтобы умножить сумму на число, можно каждое слагаемое умножить на это число, и результаты сложить.
Так, а теперь посмотрите вот на эти числовые выражения.
7 ∙ 4 + 7 ∙ 6
9 ∙ 3 + 8 ∙ 3
А здесь, как раз, складываются два произведения, в которых есть одинаковые множители.
Решаю первое из них. Семью четыре – двадцать восемь. Семью шесть – сорок два. Сумма чисел двадцать восемь и сорок два равна семидесяти.

А если попробовать распределительное свойство умножения применить в обратном порядке – сумму произведений, в которых есть одинаковый множитель, семь, заменить на произведение множителя семь и суммы чисел четыре и шесть. Пишу в скобках сумму чисел четыре и шесть, знак умножить, затем множитель семь. Сумма равна десяти, а произведение – семидесяти. Замечательно! Такое простое вычисление!
А теперь попробую найти значение второго выражения. Так, здесь одинаковый множитель три, а разные – девять и восемь. Сумму чисел девять и восемь умножу на три. Сумма равна семнадцати…. Неет, не годится здесь этот способ. Вы пока ещё не умеете умножать двузначные числа. Буду решать так, как написано. Девятью три – двадцать семь, восемью три – двадцать четыре. Сумма равна пятидесяти одному.
Ну вот, оказывается, иногда для вычисления очень удобно применять распределительное свойство умножения.
Чтобы умножить сумму на число, можно каждое слагаемое умножить на это число, и результаты сложить.
Я покажу его в виде формулы:
(a + b) ∙ c = a ∙ с + b ∙ c
Иногда удобнее применять это свойство в обратном порядке. Чтобы найти сумму двух произведений, в которых есть одинаковый множитель, можно на этот множитель умножить сумму двух других.
a ∙ с + b ∙ c = (a + b) ∙ c

Если вы научитесь применять это свойство там, где оно необходимо, вам намного легче будет решать многие примеры и задачи.
Ну, вот и пришла пора нам с вами сегодня расставаться. Но, я надеюсь, наша встреча была вам полезной, и вы будете справляться с заданиями по математике ещё быстрее и, главное, без ошибок. До свидания, ребята!

 Получите свидетельство
Получите свидетельство Вход
Вход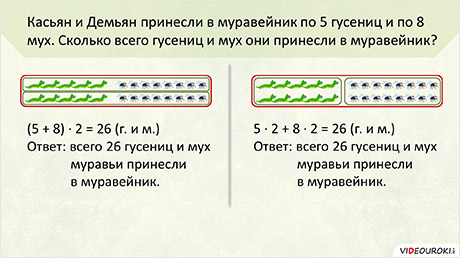




 1906
1906

