Вопросы занятия:
• ввести понятия «несовместные» и «независимые» события;
• вывести формулу вероятности суммы событий;
• вывести формулу вероятности произведения событий;
• вывести формулы Бернули и геометрической вероятности.
Материал урока
На прошлых уроках мы с вами рассматривали примеры решения простейших вероятностных задач, при этом каждый раз мы исследовали конкретную математическую модель.

Сегодня от решения простейших вероятностных задач мы перейдём к более сложным. И познакомимся с некоторыми инструментами для их решения.
Начнём с задачи.



При решении этой задачи мы применили формулу:

А так же узнали, что несовместными называют события, которые не могут произойти одновременно.

В свою очередь произведением двух событий А и Б называют событие, которое наступает тогда и только тогда, когда наступает и событие А, и событие Б.

Пример.

На этом примере мы показали, что произведение событий А и Б связано с пересечением множеств, соответствующих событиям А и Б.
В 9 классе мы говорили о связи понятий теории вероятности и теории множеств.

Запишем теорему.
Теорема 1.
Сумма вероятностей двух событий равна сумме вероятности произведения этих событий и вероятности суммы этих событий.

Это понятие одно из важнейших в теории вероятностей. И определение независимым событиям поможет дать правило умножения.
Определение.
События А и Б называют независимыми, если вероятность произведения этих событий (то есть их одновременного наступления) равна произведению вероятностей этих событий.

Вероятность суммы двух независимых событий равна разности суммы вероятностей этих событий и вероятности произведения этих событий.

Решим задачу.

Иногда проводят серию одинаковых испытаний и находят вероятность наступления того или иного события.
Определение.
Назовём наступление некоторого события А «успехом», а случай, когда оно не наступает, то есть наступает событие противоположное А «неудачей».
Вероятность события А, то есть «успеха» обозначим p, а вероятность «неудачи» — q.
Сумма противоположных событий равна одному.

Запишем теорему,
Теорема Бернулли.

Эта теорема очень важна. Применим её при решении задачи.
Пример.

Запишем ещё одну теорему.
Теорема 4.

Например, при эн большем либо равном двум тысячам с вероятностью, большей чем 99%, можно утверждать, что абсолютная погрешность разности частоты и вероятности такого приближённого равенства будет меньше 0,03.

Поэтому при социологических опросах достаточно бывает опросить около 2000 случайно выбранных людей.
Допустим, 520 из них положительно ответили на заданный вопрос. Тогда:

И практически достоверно, что для любого большего числа опрошенных такая частота будет находиться в пределах от двадцати трёх сотых до двадцати девяти сотых.

Это явление называют явлением статистической устойчивости.
Вспомним уже знакомое вам классическое определение вероятности, оно применимо к испытаниям с конечным числом исходов.
Однако часто встречаются испытания с бесконечным числом исходов. В таких случаях прибегают к геометрической вероятности.
Рассмотрим пример.
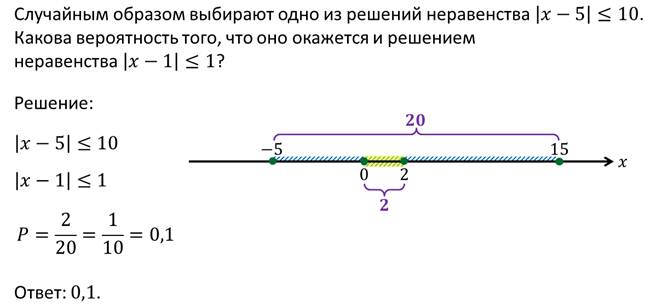
Можем сформулировать общее правило для нахождения геометрической вероятности.

Аналогично поступают и с множествами на плоскости, и с пространственными множествами. Но в этих случаях длину заменяют на площадь и объём соответственно.

Подведём итоги нашего урока.




 Получите свидетельство
Получите свидетельство Вход
Вход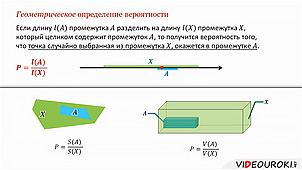



 0
0 6242
6242

