Формула бинома Ньютона

Вопросы занятия:

• вывести формулу числа сочетаний из n элементов по k;

• вывести формулу числа размещений из n элементов по k;

• познакомить с треугольником Паскаля и с закономерностью получения его чисел.

Материал урока

Вам известна формула квадрата суммы двух выражений.

Умножим это тождество на a + b.

Умножив полученное тождество на a + b ещё раз, получим:

Проанализировав полученные формулы, можно заметить, что степень каждого одночлена, записанного в правой части, равна степени многочлена a + b, записанного в левой части.

Обратите внимание.

А ещё, если вспомнить треугольник Паскаля, рассмотренный на прошлых уроках, не трудно увидеть, что коэффициенты при одночленах в правых частях построчно записаны в данном треугольнике.

Вы помните, что треугольник Паскаля состоит из значений всех возможных сочетаний.

Естественно предположить такую закономерность и для общего случая.

Эту формулу называют формулой бинома Ньютона. А коэффициенты — биноминальными коэффициентами.

Где же можно применять эту формулу?

Рассмотрим несколько примеров.

Пример.

Пример.

Пример.

А сейчас мы с вами получим одно интересное свойство.

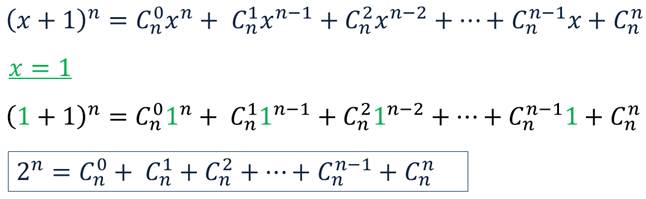
Это значит, что сумма биномиальных коэффициентов в формуле бинома Ньютона является степенью числа два.

Вернувшись к треугольнику Паскаля, это не трудно проверить.

Подведём итоги урока.

Сегодня вы познакомились с формулой бинома Ньютона. Узнали, что коэффициенты одночленов правой части составляют одну из строк треугольника Паскаля.

А также составив формулу бинома Ньютона для выражения:

Получили такое свойство биномиальных коэффициентов.