Сочетания и размещения

Вопросы занятия:

• вывести формулу числа сочетаний из n элементов по k;

• вывести формулу числа размещений из n элементов по k;

• познакомить с треугольником Паскаля и с закономерностью получения его чисел.

Материал урока

На прошлых занятиях мы работали с определением вероятности случайного события и с его помощью вычисляли вероятности.

Так же мы активно применяли правило умножения.

Из курса алгебры 9 класса вам известны понятие факториал и теорема о перестановках.

Вспомним их.

Определение.

Произведение подряд идущих первых n натуральных чисел называют n факториал.

Теорема 1.

Решим задачу.

Школьники смастерили 4 скворечника.

Сколькими способами в них могут разместиться 4 скворца?

Решение заключается в том, чтобы найти число перестановок из четырёх элементов.

Сколькими же способами в них могут разместиться 4 скворца, если один прилетела раньше всех и уже занял себе домик?

Понятно, что остаётся разместить оставшиеся 3 птицы в 3 домика.

А теперь представим себе такую ситуацию. Каждые 2 из 7 городов соединены мостами. Определим их количество.

Представим города в виде точек. Каждый мост соединяет только 2 города.

И пользуясь комбинаторным правилом умножения, число мостов можно найти так. Первый город можно выбрать семью способами, а второй — шестью. Но ведь тогда каждый мост будет посчитан два раза, а нам не важен порядок выбора городов. Значит, нужно всё разделить на два.

Запишем теорему о выборе двух элементов.

Теорема 2.

Определение.

Тогда теорему 2 кратко можно записать в виде формулы.

Решим задачу.

Рассмотрим другую ситуацию.

Пример.

Теорема 3.

Определение.

Тогда теорему можно записать так:

Решим задачу.

Запишем определения.

Число всех выборов k элементов из n данных без учёта порядка называют числом сочетаний из n элементов по k.

Число всех выборов k элементов из n данных с учётом их порядка называют числом размещений из n элементов по k.

Как же находить число сочетаний и размещений из n элементов по k?

Запишем теорему.

Теорема 4.

Для любых натуральных чисел n и k, таких, что k < n, справедливы следующие соотношения.

Этими формулами мы и будем пользоваться при вычислении числа сочетаний и размещений.

Решим уравнение.

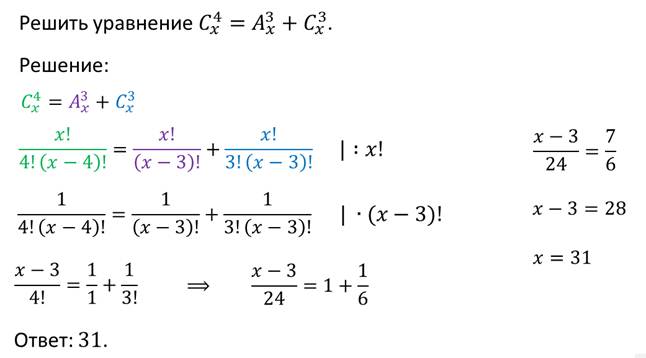
Так мы с помощью изученных формул решили уравнение, а теперь решим задачу.

Пример.

Для чисел сочетаний из эн элементов по ка существует красивый и удобный способ их записи с помощью треугольной таблицы, её называют треугольник Паскаля.

Он выглядит так.

Закономерность образования строк заключается в следующем: каждое число в треугольнике Паскаля равно сумме двух чисел, стоящих над ним в предыдущей строке. 5=1+4, 10=4+6, 6=3+3 и так далее.

Кратко эту закономерность можно записать в виде такой формулы.

Подведём итоги нашего урока.

Сегодня мы рассмотрели такие инструменты комбинаторики как сочетание и размещение.

Познакомились с формулами отыскания числа сочетаний и размещений из эн элементов по ка. Выяснили, в чём их отличие друг от друга.

А также рассмотрели примеры решения задач с помощью этих инструментов.