Вопросы занятия:
· вспомнить, что такое числовое неравенство, неравенство с переменными, линейное неравенство с одной и двумя переменными;
· повторить способы решения линейных неравенств.
Материал урока
Но прежде, давайте вспомним, что такое числовое неравенство.
Определение.
Числовым неравенством называется символическая запись, в которой два числа или числовых выражения связаны одним из знаков сравнения.

Напомним, что:


Определение.
Решением неравенства с одной переменной называется такое значение переменной, при подстановке которого неравенство обращается в верное числовое неравенство.
Определение.
Решить неравенство – значит найти все его решения или доказать, что решений нет.
Определение.
Равносильными называются неравенства, множества решений которых совпадают.
Равносильными неравенства получаются, если:

Теперь давайте повторим основные свойства числовых неравенств.

Неравенство с переменными может при одних значениях переменных быть верным, при других – нет.
Определение.
Доказать неравенство – значит, доказать, что оно имеет место при всех допустимых значениях переменных.
Как правило, для доказательства неравенств используют метод составления разности между левой и правой частями и оценки её знака.
Рассмотрим пример.
Пример.

Определение.
Линейные неравенства – это неравенства вида:

Особенностью линейных неравенств является то, что в таких неравенствах х присутствует только в первой степени, нет деления на х и х не стоит под знаком корня.
Как правило, решениями линейных неравенств являются числовые промежутки. Давайте немного вспомним, как связаны числовые неравенства с числовыми промежутками.
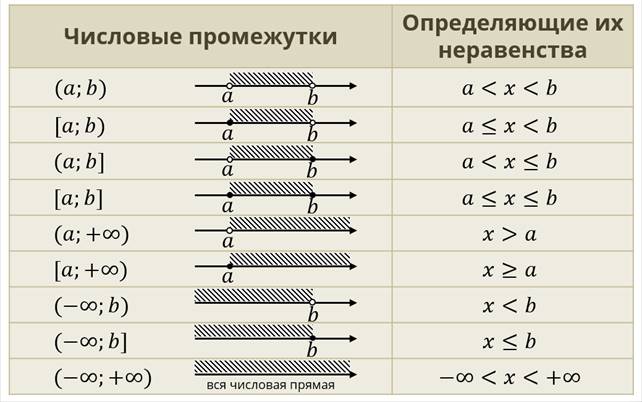
Если неравенство строгое, то концы промежутка на числовой прямой будут «выколотыми» и при записи в виде интервала, скобки будут круглыми. Если же неравенства нестрогие, то на числовой прямой концы интервала будут закрашены, а интервал берётся в квадратные скобки.
Рассмотрим пример.
Пример.
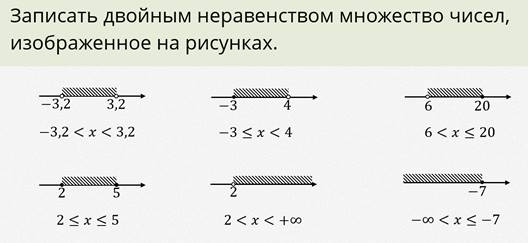
В зависимости от знака коэффициентов решениями линейных неравенств будут разные промежутки.

Рассмотрим несколько примеров.
Пример.

Пример.

Рассмотрим ещё один пример.
Пример.
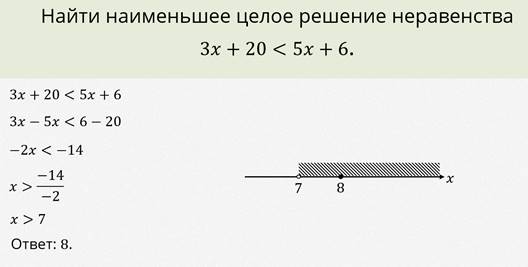
Пример.

Пример.

Пример.

Часто приходится решать линейные неравенства с двумя переменными.
Определение.
Линейные неравенства с двумя переменными – это неравенства вида

Заметим, что обе переменные должны быть в первой степени.
Определение.
Решением неравенства с двумя переменными называется пара значений этих переменных, обращающая данное неравенство в верное числовое неравенство.
Так как неравенство с двумя переменными имеет множество решений, то их сложно перечислить. Увидеть множество решений неравенства с двумя переменными позволяет график.

Итоги урока
Сегодня мы вспомнили, что такое числовое неравенство, неравенство с переменными, линейное неравенство с одной и двумя переменными. Вспомнили, как решаются такие неравенства.

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 6394
6394

