Числовые неравенства

Вы уже научились сравнивать любые числа, в каком бы виде они не были записаны. Результат их сравнения  записывают в виде равенства или неравенства. Причём, используют следующие знаки: равно, меньше, больше.

Для произвольных чисел  и  верно одно и только одно из трех соотношений:

Пусть  и  – некоторые выражения.

Определение:

Если два выражения,  и , соединить одним из знаков, то полученную записи называют неравенством:

Определение:

Когда обе части неравенства обозначают числа, то такое неравенство называется числовым.

Числовое неравенство  называется верным, если его левая часть обозначает число, меньшее, чем правая.

Числовое неравенство  называется верным, если его левая часть обозначает число, большее, чем правая.

Давайте вспомним, как сравнивают конкретные числа.

При сравнении натуральных чисел сравнивают их разряды.

При сравнении дробей – приводят их к общему знаменателю.

При сравнении отрицательных чисел сравнивают их модули.

Как сравнивают числовые выражения понятно, а вот как сравнить выражения, например,  и ? Для этого составляют разность выражений и выясняют, является ли она положительным числом, отрицательным числом или нулём.

Определение:

Число  больше числа , если разность  – положительное число.

Число 𝒂 меньше числа 𝒃, если разность  – отрицательное число.

Если разность , то числа .

Также вы умеете сравнивать числа при помощи координатной прямой. Напомним, что на координатной прямой большее число изображается точкой, лежащей правее, а меньшее – точкой, лежащей левее.

Действительно,

Давайте рассмотрим, как используется данное определение, при выполнении заданий.

Задание: сравните числа  и , если:

Решение:

Задание 2: докажите, что при любых значениях переменной верно неравенство.

Решение:

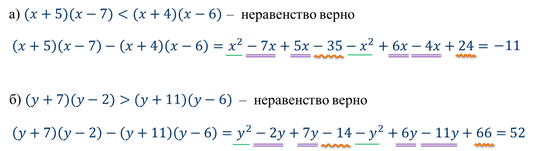
И, напоследок, давайте докажем, что что , при условии, что .

Решение:

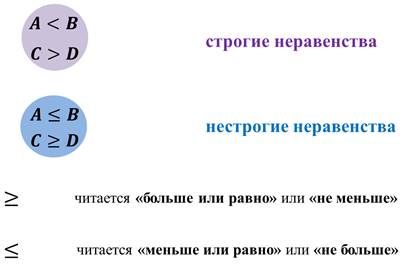
Итоги:

Два выражения, соединённые знаками , , , или  называют неравенствами.

Когда обе части неравенства обозначают числа, то такое неравенство называется числовым.

Число 𝒂 больше числа 𝒃, если разность 𝒂−𝒃 – положительное число.

Число 𝒂 меньше числа 𝒃, если разность 𝒂−𝒃 – отрицательное число.