Получите свидетельство
Вход
«Кто овладел творениями Архимеда,
будет меньше удивляться открытиям
самых великих людей нашего времени»
Г.В. Лейбниц
Данная тема посвящена решению задач на тему «Блоки. Условие равновесия блоков».
Задача 1. Какую минимальную силу нужно приложить к концу веревки для подъема мешка цемента массой 50 кг с помощью данной системы блоков? На какую высоту будет поднят мешок при совершении этой силой работы в 2500 Дж? Считать блоки идеальными.
|
ДАНО:
|
РЕШЕНИЕ:
Подвижный блок, позволяет получить выигрыш в силе в два раза. Значит, минимальная сила, которую нужно приложить к концу веревки для подъема мешка цемента, равна половине веса этого мешка
Вес мешка цемента:
Тогда минимальная сила
Работа силы определяется по формуле
Согласно «Золотому правилу механики», если мы выигрываем в силе, то во столько же раз проигрываем в пути. Так как подвижный блок дает нам выигрыш в силе в два раза, то в пути мы проиграем также в два раза, то есть высота подъема мешка цемента будет в два раза меньше высоты подъема точки приложения силы
Высоту подъема точки приложения силы определим как отношение работы, совершенной силой, к модулю этой силы
Тогда искомая высота
|
|
|
Ответ: 250 Н; 5 м.
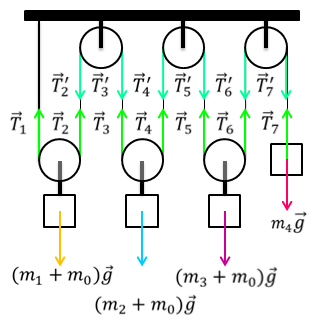
Задача 2. В системе, изображенной на рисунке, масса самого правого груза равна 1,5 кг, а массы всех блоков одинаковы и равны 0,4 кг. Система уравновешена и неподвижна. Определите массы остальных грузов, если массой троса и трением в блоках можно пренебречь.
|
ДАНО:
|
РЕШЕНИЕ:
Если трос является невесомым и нерастяжимым, а так же при отсутствии трения в блоках, силы натяжения троса должны быть равны между собой
Поскольку система уравновешена, то:
С другой стороны, трос передает производимое на него воздействие равномерно по всей своей длине. Так как на блоки с обеих сторон действуют силы натяжения T, а на ось каждого блока действует вес подвешенного на него груза и вес самого блока, то получаем, что в равновесии сила тяжести, действующая на каждый из блоков с грузом, уравновешивается удвоенной силой натяжения троса
Поскольку система уравновешена, то:
|
|
|
Ответ: 2,6 кг.
Задача 3. Плита массой 120 кг была равномерно поднята с помощью подвижного блока на высоту 16 м за 40 с. Считая КПД механизма 80%, а массу блока — 10 кг, определите полную работу и развиваемую мощность. Считать, что в блоке отсутствуют силы трения.
|
ДАНО:
|
РЕШЕНИЕ:
Коэффициента полезного действия механизма определяется отношением полезной работы механизма ко всей затраченной им работе
Полезная работа:
Сила тяжести плиты и блока:
Тогда
Затраченная работа:
Затраченная мощность:
|
|
|
Ответ: 26 кДж; 650 Вт.
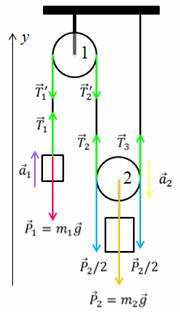
Задача 4. На рисунке изображена система грузов. Массы тел соответственно равны 0,2 кг и 0,4 кг. Определите силу натяжения нити. Считать нить и блоки идеальными?
|
ДАНО:
|
РЕШЕНИЕ:
Так как нить и блоки идеальны, то:
На основании II закона Ньютона:
Так как блок 2 подвижный:
Тогда получаем
Выразим из второго уравнения ускорение a2, подставим полученное выражение в первое уравнение
Преобразуем полученное уравнение и выразим из него искомую силу натяжения нити
|
|
|
Ответ: 2 Н.
0
19192
