Методы решения физических задач по статике

«Равновесие получается в результате

уничтожения нескольких сил, которые

борются и взаимно сводят на нет действие,

производимое ими друг на друга; статика

имеет своей целью дать законы, согласно

которым происходит это уничтожение».

Ж.Л. Лагранж

В данной теме разговор пойдёт об элементах статики, вспомним основные формулы, связанные с данным разделом физики, а также дадим некоторые рекомендации по решению задач на данную тему.

Статика — это раздел физики, который изучает равновесия материальной точки и абсолютно твердого тела.

Абсолютно твердое тело — это тело, размеры и форму которого можно считать неизменными.

Условия равновесия — это условия, при которых тело при наличии внешних воздействия может находиться в покое относительно инерциальной системы отсчета; двигаться поступательно, равномерно и прямолинейно; равномерно вращаться относительно оси, проходящей через центр масс.

Основные физические величины, используемые в статике, — это сила и момент силы.

Сила — это векторная физическая величина, описывающая и измеряющая воздействие одного тела на другое, в результате которого тела приобретают ускорение или деформируются. Она характеризуется: модулем, направлением в пространстве и точкой приложения.

При осуществлении различных операций над силами необходимо всегда помнить, что точку приложения силы можно переносить только вдоль прямой, вдоль которой эта сила действует.

Важным понятием является и понятие равнодействующей силы, то есть силы, которая производит на тело такое же действие, как и несколько одновременно действующих на него сил. Она равна геометрической сумме этих сил. Иными словами, сложить силы — это значит найти их равнодействующую.

Рассмотрим некоторые правила сложения сил. Начнем со сложения параллельных сил. Представим, что имеется некое твердое тело, которое изобразим в виде прямоугольника, на концы которого действую две силы, направленные в одну и ту же сторону параллельно друг другу. Для того, чтобы найти равнодействующую этих двух сил, необходимо параллельным переносом совместить конец одного вектора с началом второго.

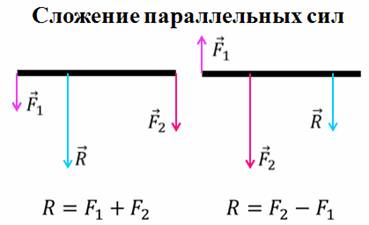
Из рисунка хорошо видно, что равнодействующая двух параллельных одинаково направленных сил равна по модулю сумме их модулей, параллельна им и направлена в ту же сторону. Помимо этого, линия действия равнодействующей силы делит отрезок, соединяющий точки приложения слагаемых сил, на участки, обратно пропорциональные силам.

Теперь вспомним, как найти равнодействующую двух антипараллельных сил, то есть сил, которые параллельны друг другу, но направлены в противоположные стороны. Как и в предыдущем случае, нам необходимо параллельным переносом совместить конец одного вектора силы с началом вектора другой силы. Из рисунка видно, что равнодействующая двух антипараллельных сил равна по модулю разности их модулей, параллельна им и направлена в сторону большей силы. При этом точка приложения равнодействующей лежит на продолжении линии, соединяющей точки приложения слагаемых сил на расстояниях от них, обратно пропорциональных силам.

Теперь вспомним, как найти равнодействующую не параллельных сил. Пусть к некоторому телу приложено две силы в одной точке, направленные под некоторым углом альфа друг к другу. Тогда их равнодействующую находят по правилу параллелограмма.

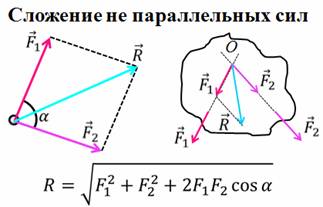
Если же непараллельные силы приложены в разных точках тела, то для нахождения их равнодействующей поступают следующим образом: сначала проводят прямые, вдоль которых действуют эти силы, до их пересечения в некоторой точке. Затем, действующие силы переносят в точку пересечения прямых, вдоль которых они действуют. А затем производят их векторное сложение по правилу параллелограмма. При этом точкой приложения равнодействующей силы может быть любая точка прямой, вдоль которой эта сила действует.

Модуль равнодействующей двух непараллельных сил можно определить по теореме косинусов. А если угол между векторами сил равен девяносто градусов, то по теореме Пифагора.

Теперь поговорим об условиях равновесия. Начнем с равновесия тела, которое не имеет оси вращения. Если под действием приложенных к телу сил оно движется поступательно, то все его точки движутся одинаково и достаточно рассмотреть движение одной точки. Условие равновесия такого тела, как и условие равновесия материальной точки, вытекает из основного уравнения динамики: чтобы не вращающееся тело находилось в равновесии, необходимо, чтобы геометрическая сумма сил, действующих на тело, была равна нулю (или алгебраическая сумма проекций этих сил на оси координат была равна нулю).

Если же тело, под действием приложенных к нему сил поступательно не движется, а поворачивается вокруг некоторой закрепленной оси, то для его равновесия необходимо выполнения следующего условия: алгебраическая сумма моментов сил, приложенных к телу, относительно оси вращения, должна равняться нулю.

Момент силы — это произведение модуля силы на ее плечо, то есть на кратчайшее расстояние от оси вращения до линии действия силы. Обратите внимание: не до точки приложения силы, а именно до линии, вдоль которой действует сила. При этом принято считать момент силы положительным, если сила вращает тело относительно данной оси по ходу часовой стрелки, и отрицательным, если сила вращает тело против хода часовой стрелки.

В общем случае, если тело под действием приложенных к нему сил может и поворачиваться, и двигаться поступательно, то для того, чтобы оно находилось в равновесии, необходимо выполнение данных двух условий одновременно.

Для того чтобы судить о поведении тела в реальных условиях, мало знать, что оно находится в равновесии. Надо еще оценить это равновесие. Поэтому различают три вида равновесия: устойчивое равновесие, неустойчивое равновесие и безразличное равновесие.

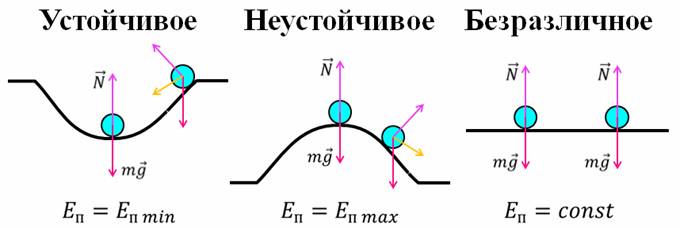
Равновесие тела называют устойчивым, если при отклонении от него возникают силы, возвращающие тело в положение равновесия.

Неустойчивым называют такое равновесие тела, при котором даже самое незначительное отклонение от положения равновесия, равнодействующая действующих на тело сил вызывает дальнейшее отклонение тела.

А вот равновесие, при котором смещение тела в любом направлении не вызывает изменений действующих на него сил и равновесие тела сохраняется, называют безразличным.

Объяснение видов равновесия может быть дано и на основании определения центра тяжести (или центра масс) тела. Центр тяжести — это такая точка приложения равнодействующей сил тяжести, действующих на все части тела, которая не изменяет своего положения при любых поворотах тела.

Таким образом, в устойчивом равновесии центр тяжести тела занимает наинизшее из всех возможных положений и связан с минимум потенциальной энергии по отношению ко всем близким соседним положениям тела.

При неустойчивом равновесии высота центра тяжести максимальна, как максимальна и потенциальная энергия по отношению к другим близким положениям тела.

Безразличное равновесие связано с неизменной потенциальной энергией всех близких состояний, и высота центра тяжести одинакова во всех достаточно близких положениях.

Сведем в таблицу основные формулы элементов статики.

Методические рекомендации по решению задач, относящихся к равновесию тел

1) Проанализировав условие задачи, сделать чертеж с указанием на нем всех сил, действующих на тело, находящееся в положении равновесия.

Задача. Однородный деревянный кубик массой т находится на наклонной плоскости. Определите действующую на него силу трения покоя.

Во-первых, рисуем рисунок, на котором указываем наклонную плоскость и кубик на ней,а затем указываем действующие на кубик силы: силу тяжести, силу нормальной реакции плоскости и силу трения покоя. Исходя из рисунка, делаем вывод о том, что данная задача является задачей на условие равновесия тела, не имеющего оси вращения.

2) Для тела, не имеющего оси вращения, достаточно использовать первое условие равновесия, которое говорит нам о том, что геометрическая сумма приложенных к телу сил должна равняться нулю.

3) Выбрать оси координат и записать это уравнение в проекциях.

4) Для тела с закрепленной осью вращения достаточно использовать правило моментов, согласно которому, тело с закрепленной осью вращения будет находиться в равновесии, если алгебраическая сумма моментов всех сил, действующих на тело, будет равна нулю.

Для этого надо найти плечи всех сил относительно данной закрепленной оси. А затем составить алгебраическую сумму моментов этих сил с учетом знаков и приравнять ее к нулю.

5) Если ось вращения тела не закреплена, то необходимо использовать оба условия равновесия. Для конкретного примера, используем то, что алгебраическая сумма проекций сил на оси координат должна равняться нулю.

6) Для записи правила моментов необходимо выбрать ось вращения. Лучше ее выбирать так, чтобы через нее проходило наибольшее число линий действия неизвестных сил. Тогда моменты этих сил, относительно выбранной точки, будут равны нулю.

7) Необходимо решить полученную систему уравнений относительно искомой величины.